1. Chữ U ngược là kí hiệu gì trong toán học?
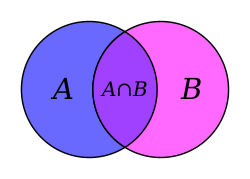
Chữ U ngược kí hiệu này là “hợp lại” :
VD : {3} ∪ {x| x < 2}
Có nghĩa là hai tập hợp này hợp lại thì bằng số nghiệm của 1 phương trình đã cho nào đó. Kí hiệu chữ u ngược như thế và “giao nhau”.
2. Tổng hợp một số kí hiệu trong toán học?
Tập hợp
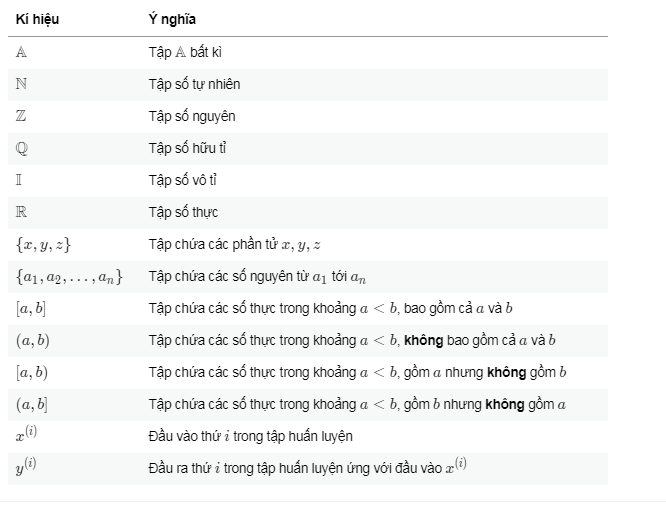
Số và ma trận:
Giải tích:

Xác suất thống kê:






























[…] Chữ u ngược là ký hiệu gì trong toán học? Tổng… […]
[…] r là số gì trong toán học >>> u là gì trong toán học >>> n* nghĩa là gì trong toán học? >> x là gì trong toán […]
[…] Chữ u ngược là ký hiệu gì trong toán học? Tổng hợp kí hiệu toán học […]
[…] >>> Chữ u ngược là ký hiệu gì trong toán học? Tổng hợp kí hiệu toán học […]
[…] >>> Chữ u ngược là ký hiệu gì trong toán học? […]
[…] >> Chữ u ngược là ký hiệu gì trong toán học […]