1. ln trong toán học là gì?
Trong danh sách toán học tại Việt Nam lnx là kí hiệu để chỉ “logarit tự nhiên”. Logarit tự nhiên là Logarit cơ số e do nhà Toán học đại tài John Napier sáng tạo ra, ta thường gặp 2 kí hiệu của thuật ngữ này là ln(x) hoặc là log(x).
“ln” rất quan trọng trong toán học và các ứng dụng thực tiễn, nó giúp chúng ta giải các phương trình mũ, phân tích dữ liệu lãi suất kép, cấp số nhân, phân rã, và tích hợp hàm số….
Logarit tự nhiên là logarit cơ số e, trong đó e là hằng số Euler, xấp xỉ bằng 2.71828.

2. Tính chất của ln trong toán học?
– Tính chất cơ bản:
- ln(1)=0
- ln(e)=1 rong đó e là hằng số Euler, xấp xỉ 2.71828.
– Tính chất đồng nhất:
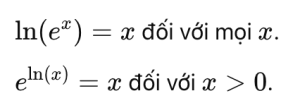
– Tính chất cộng:
- ln(ab)=ln(a)+ln(b) đối với a > 0 và b > 0
– Tính chất hiệu:
![]()
– Tính chất lũy thừa:
![]()
– Đạo hàm:
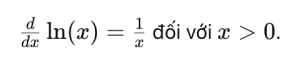
– Nguyên hàm:
![]()
– Đồng biến:
- Hàm số ln(x) là hàm đồng biến trên khoảng (0,∞) nghĩa là nếu 0<a<b thì ln(a) .
– Giới hạn:
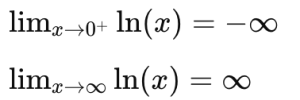
– Tính liên tục và khả vi:
- Hàm ln(x) liên tục và khả vi trên khoảng (0,∞).
3. Bài tập ví dụ về ln trong toán học?
Bài 1: Cho a > 0,a ≠ 1, biểu thức A=(lna+logae)2+ln2a – (logae)2 có giá trị bằng:
A. 2ln2a+2
B. 4lna+2
C. 2ln2a-2
D. ln2a + 2
Đáp án: A
Bài 2: Cho log3x = 4log3a + 7log3b (a, b > 0). Giá trị của x tính theo a,blà :
A. ab
B. a4b
C. a4b7
D. b7
Đáp án: C
Bài 3: Giá trị của ln(1) là bao nhiêu?
A. 1
B. 0
C. e
D. ∞
Đáp án: B
Bài 4: Giải phương trình 2ln(x)=ln(16)
A. x=4x
B. x=16x
C. x=8x
D. x=2x
Đáp án: A. x=4x
Bài 5: Giá trị của ln(10)≈(Sử dụng giá trị gần đúng)
A. 2.718
B. 2.302
C. 1
D. 0.301
Đáp án: B. 2.302
4. Tìm hiểu thêm về giáo trình ln?