Trong môn giải tích thì chắc chắn các bạn đã làm quen với định nghĩa về sup rồi. Hôm nay mình sẽ chia sẻ cho các bạn về “sup trong toán học” là gì? và một số ví dụ bài tập về sup cho các bạn tìm hiểu?
1. Sup trong toán học là gì?
Định nghĩa: Trong giải tích, cận trên đúng hay cận trên nhỏ nhất của một tập các số thực S được ký hiệu là sup(S) và được định nghĩa là số thực nhỏ nhất mà lớn hơn hoặc bằng với mọi số trong S. Một tính chất quan trọng của tập số thực là tính đủ: mọi tập con không rỗng của tập số thực mà bị chặn trên thì có một cận trên đúng và cận trên đúng này cũng là một số thực.
2. Bài tập về sup?
Cho bài tập như sau:
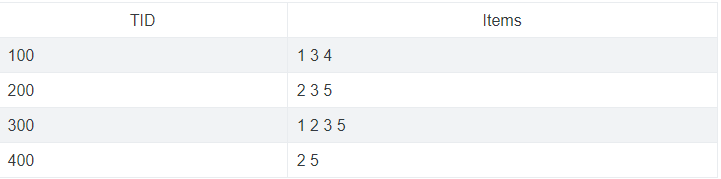
Tìm các tập mục có độ hỗ trợ ≥ 0.5 (tức tần số sup. ≥ 2).
Lý thuyết
Các định nghĩa cơ bản
Tập hạng mục (Itemset)
Giả sử I là một tập hữu hạn, mỗi phần tử của I gọi là một hạng mục (Item).
Một tập hạng mục X là một tập con của I.
X gọi là một tập hạng mục mức k (k_itemset) nếu X chứa k hạng mục.
Ví dụ: I = {1 2 3 4 5}; 1, 2, 3, 4, 5 là các hạng mục; X = {2 5} là một tập hạng mục mức 2.
Giao dịch (Transaction)
Một tập các giao dịch xác định trên I là một ánh xạ T:{1,2,..,n} → P(I). Tập T(k) là giao dịch thứ k của T.
Các số 1,..,n là các định danh giao dịch (tids).
Ví dụ: giao dịch thứ 100, Tids(100) = {1 3 4}.
Ký hiệu tập các giao dịch chứa tập hạng mục
Giả sử X = {1 3}, tập các định danh giao dịch có chứa X là {100, 300}, kí hiệu là λ(X):
Độ hỗ trợ (Support)
Độ hỗ trợ của một item set X ký hiệu là sup(X) được xác định bởi công thức:
Ví dụ: sup({1 3}) = 2/4 = 1/2.
Tập phổ biến/ tập thường xuyên (Large itemset/frequent itemset)
Một itemset X được gọi là phổ biến hay tập thường xuyên nếu:
trong đó 𝛿: minsup là một ngưỡng do người dùng xác định.
Ngược lại thì X được gọi là tập không phổ biến (small itemset)
Luật kết hợp
Một luật kết hợp là một công thức có dạng X ⇒ Y, trong đó X, Y là hai itemset thoả X ∩ Y = ∅, X được gọi là tiền đề và Y được gọi là hệ quả của luật.
Ví dụ: 2 ⇒ {3 5}.
Luật kết hợp chỉ có ý nghĩa khi tần suất thể hiện mối tương quan giữa các tập thuộc tính là lớn hơn một ngưỡng nào đó.
Độ hỗ trợ của luật kết hợp
Độ hỗ trợ của một luật X ⇒ Y, ký hiệu sup(X ⇒ Y) là khả năng mà tập giao dịch T hỗ trợ cho các thuộc tính trong cả X và Y.
Độ tin cậy của luật kết hợp
Độ tin cậy của một luật X ⇒ Y, ký hiệu conf(X ⇒ Y) là xác suất có điều kiện :
Ví dụ: xét luật kết hợp 2 ⇒ {3 5}, ta có sup(2 ⇒ {3 5}) = 2/4 = 1/2, conf(2 ⇒ {3 5}) = 2/3.
Các tính chất
Các tính chất của large itemset
Nếu và là các Itemset thì .
Tính chất Apriori
- Mọi tập con của một tập phổ biến đều phổ biến, nghĩa là:
- Mọi tập mẹ của một tập không phổ biến đều không phổ biến, nghĩa là:
Đặt vấn đề
Với một tập giao dịch T, mục đích của bài toán phát hiện luật kết hợp là tìm ra tất cả các luật có:
- độ hỗ trợ ≥ minsup và
- độ tin cậy ≥ minconf.
Thuật toán gồm hai bước:
- Sinh ra các tập mục phổ biến có độ hỗ trợ ≥ minsup.
- Sinh ra các luật kết hợp:
- Từ mỗi tập mục phổ biến, sinh ra tất cả các luật có độ tin cậy cao (≥ minconf).
- Mỗi luật là một phân tách nhị phân của một tập mục phổ biến.
Bước sinh ra các tập mục phổ biến có độ phức tạp cao, chúng ta tập trung vào bài tập tìm tập mục phổ biến (các tập có độ hỗ trợ ≥ minsup).
Thuật toán Apriori
Thuật toán do Agrawal đề nghị năm 1994, ý tưởng của thuật toán dựa vào tính chất Apriori: các ứng viên k+1_itemset có độ hỗ trợ ≥ μ, phải được sinh ra từ các k_itemset có độ hỗ trợ ≥ μ.
Xem lời giải dưới đây để hiểu cách triển khai thuật toán.
Lời giải
Đầu tiên tìm ra các itemset mức 1 và tính sup. của chúng dựa vào dữ liệu đã cho, đây gọi là tập ứng viên mức 1 – C1:
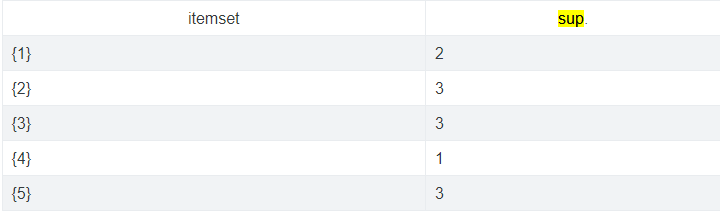
Loại những itemset có sup. < 2, tập những itemset này kí hiệu là L1:
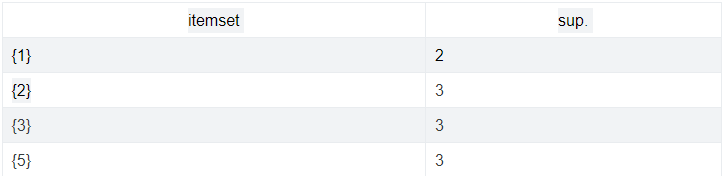
Những itemset mức 2 có sup. ≥ 2 chỉ có thể sinh ra từ những itemset mức 1 có sup. ≥ 2 (tức những itemset mức 1 vừa liệt kê), liệt kê các itemset mức 2 có thể (C2) và tính sup. tương ứng:
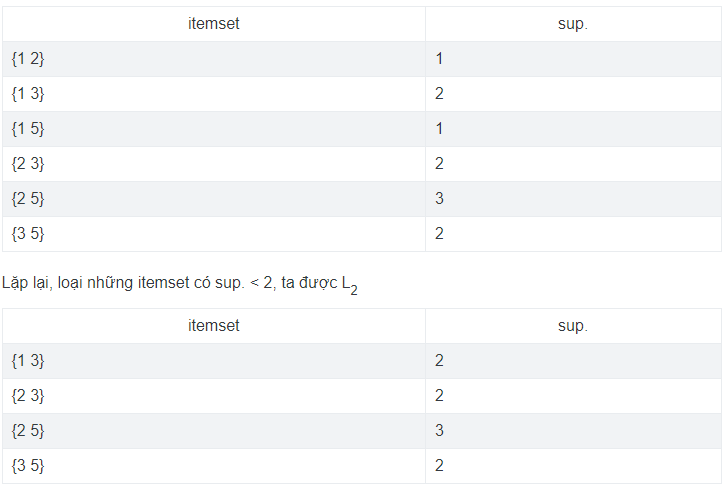
Tính tập ứng viên C3:
- Bước tổ hợp: {1 2 3}, {1 2 5}, {2 3 5}.
- Bước tỉa:
- loại {1 2 3}, vì {1 2 3} sinh ra {1 2} không thuộc L2.
- loại {1 2 5}, vì {1 2 5} sinh ra {1 2} không thuộc L2.
- giữ {2 3 5}, vì các tập con của {2 3 5} là {2 3}, {2 5}, {3 5} đều thuộc L2.
Vậy tập ứng viên C3 và sup. tương ứng: