1. Lim trong toán học là gì?
- Lim – viết tắt của Limit trong tiếng anh với nghĩa là “giới hạn”. Định nghĩa về “giới hạn” được sử dụng để chỉ giá trị mà một hàm số hoặc một dãy số tiến gần đến khi biến số tương ứng tiến gần đến một giá trị nào đó.
- Khái niệm về giới hạn cho phép ta xác định một điểm mới từ một dãy Cauchy các điểm đã được xác định trước trong một không gian đầy đủ. Giới hạn được xem là một khái niệm quan trọng của môn Giải tích và được sử dụng để định nghĩa về tính liên tục, đạo hàm và phép tính tích phân.
- Định nghĩa về giới hạn dãy số được tổng quát hóa thành giới hạn của một lưới topo, và được liên hệ chặt chẽ với các khái niệm giới hạn và giới hạn trực tiếp trong lý thuyết phạm trù. Ký hiệu giới hạn bằng chữ lim.
- Ví dụ để chỉ a là giới hạn của dãy số
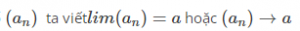
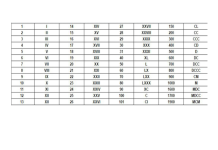
2. Giới hạn 0

3. Giới hạn của hàm số tại một điểm
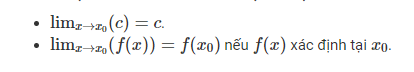
4. Giới hạn của hàm số tại vô cực
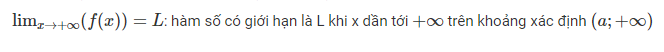
5. Giới hạn của hàm số là Lim

có nghĩa là f(x) sẽ càng gần L nếu x đủ gần c. Trong trường hợp này, ta nói giới hạn của f(x), khi x đạt đến c là L. Cần chú ý rằng điều này cũng đúng cả khi f(c) ≠ L cũng như khi hàm số f(x) không xác định tại c. Ví dụ, xét hàm số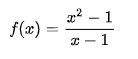
thì f(1) không xác định nhưng khi x tiến tới 1 thì f(x) tiến tới 2:
Như vậy, f(x) có thể gần 2 một cách tùy ý, chỉ cần cho x đủ gần 1.
Karl Weierstrass đã hình thức hóa định nghĩa giới hạn hàm số bằng phương pháp (ε, δ) vào thế kỉ 19.
Ngoài trường hợp hàm số f(x) có giới hạn tại một điểm hữu hạn, hàm số f(x) còn có thể có giới hạn tại vô cực. Ví dụ, xét hàm số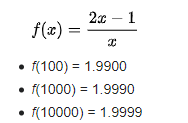
Khi x trở nên vô cùng lớn thì giá trị của f(x) tiến dần đến 2, và giá trị của f(x) có thể gần 2 một cách tùy ý, chỉ cần cho x đủ lớn. Ta nói “giới hạn của hàm số f(x) tại vô cực bằng 2” và viết.
![]()
>> Linear trong toán học là gì?