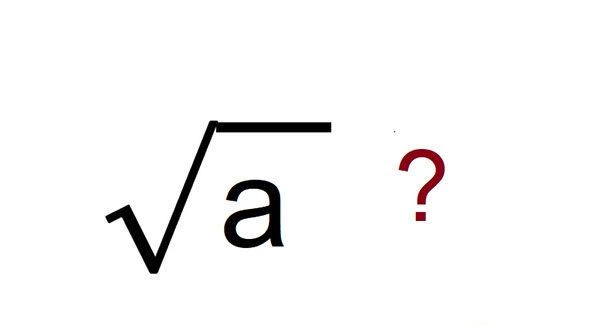1. Căn trong toán học nghĩa là gì?
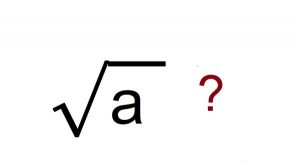
Căn trong toán học là từ nói nhanh của căn bậc hai chúng ta đã được học ở lớp 9 và lớp 7.
Căn thức bậc hai : Với A là một biểu thức đại số, A−−√ người ta gọi là Căn thức bậc hai của A, còn A được gọi là biểu thức lấy căn hay biểu thức dưới căn
Căn bậc hai của một số a là một số x sao cho x2 = a, hay nói cách khác là số x mà bình phương lên thì bằng a.

2. Tính chất và ý nghĩa của căn bậc 2 trong toán học?
- Mọi số thực a không âm đều có một căn bậc hai không âm duy nhất, gọi là căn bậc hai chính, ký hiệu a−−√. Ở đây, √ được gọi là dấu căn.
- Ví dụ: căn bậc hai chính của 9 là 3, ký hiệu 9–√ = 3, vì 32 = 3 × 3 = 9 và 3 là số không âm.
- Mọi số dương a đều có hai căn bậc hai: a−−√ là căn bậc hai dương và −a−−√ là căn bậc hai âm. Chúng được ký hiệu đồng thời là ±a−−√.
- Mặc dù căn bậc hai chính của một số dương chỉ là một trong hai căn bậc hai của số đó, việc gọi “căn bậc hai” thường đề cập đến căn bậc hai chính. Đối với số dương, căn bậc hai chính cũng có thể được viết dưới dạng ký hiệu lũy thừa, như là a12.
- Hàm số căn bậc hai chính f(x) = x−−√ (thường chỉ gọi là “hàm căn bậc hai”) là một hàm số vạch ra tập hợp các số không âm. Căn bậc hai của x là số hữu tỉ khi và chỉ khi x là số hữu tỉ và có thể biểu diễn dưới dạng tỉ số căn bậc hai của hai số chính phương.
- x2−−√ = ∣x∣
- = x nếu x≥0
- = -x nếu x<0
- Với hai số a và b không âm, ta có:
- a<b <=> a−−√<b√.
- xy−−√ = x−−√. y√
3. Định nghĩa căn bậc hai của một số âm và số phức
- Căn bậc hai của một số âm là số chỉ tồn tại trong một tập hợp bao quát hơn gọi là tập số phức.
- Bình phương của mọi số dương và âm đều là số dương, và bình phương của 0 là 0. Bởi vậy, không số âm nào có căn bậc hai thực.
- Một số mới, ký hiệu là i (đôi khi là j, đặc biệt trong điện học, ở đó “i” thường được dùng để mô tả dòng điện), gọi là đơn vị ảo, được định nghĩa sao cho i2 = – 1. Từ đây ta có thể tưởng tượng i là căn bậc hai của – 1, nhưng để ý rằng (−i)2 = i2 = – 1 do đó – i cũng là căn bậc hai của – 1. Với quy ước này, căn bậc hai chính của -1 là i. Hay tổng quát hơn, nếu x là một số không âm bất kỳ thì căn bậc hai chính của – x là −x−−−√ = ix−−√
- Đối với mọi số phức z khác 0 tồn tại hai số w sao cho w2 = z căn bậc hai chính của z và số đối của nó.