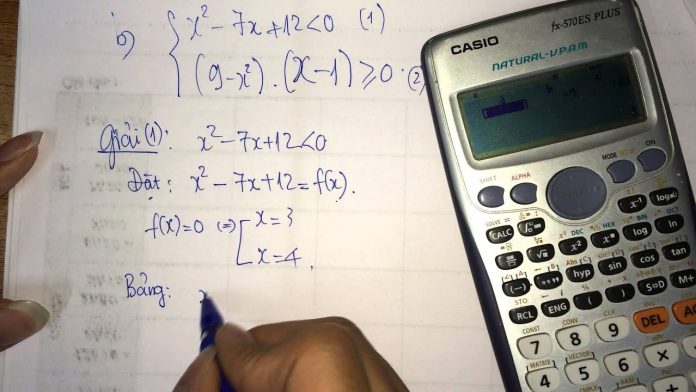Giải bất phương trình? và cách giải hệ bất phương trình?

By
admin
-
0
1410
Giải bất phương trình?và cách giải hệ bất phương trình?

Mục lục bài viết

1. Bất phương trình là gì? Ví dụ về bất phương trình

Ví dụ về bất phương trình:

2x + 3 ≥ -6

  • Vế trái của bất phương trình: 2x + 3
  • Vế phải của bất phương trình: -6

Bất phương trình có hai vế không bằng nhau, có thể lớn hơn hoặc nhỏ hơn. Nghiệm của bất phương trình không phải chỉ là một giá trị mà sẽ bao gồm cả một tập hợp giá trị thỏa mãn điều kiện của bất phương trình.

Có rất nhiều dạng bất phương trình khác nhau như : bất phương trình bậc một, bất phương trình bậc hai, bất phương trình vô tỷ, bất phương trình chứa căn, bất phương trình logarit. Mỗi dạng bài lại có một cách giải bất phương trình khác nhau, tùy theo đặc điểm của bất phương trình.

Nhưng bên trên mình đã ví dụ cho các bạn một cách dễ hiểu nhất về bất phương trình rồi. Các bạn có thể tham khảo.

2. Các dạng của bất phương trình:

* Bất phương trình tương đương

1. Định nghĩa: hai bất phương trình được gọi là tương đương nhau nếu chúng có cùng tập nghiệm.

2. Định lý

2.1 Định lý 1 (phép cộng, trừ):

Cho f(x) > g(x) xácđịnh trên D. Nếu h(x) xác định trên D thì: f(x) > g(x) <=> f(x) + h(x) > g(x) + h(x)

*  Hệ quả: Nếu chuyển một biểu thức từ vế này sang vế kia của phương trình và đổi dấu thì ta được một bất phương trình mới tương đương với phương trình đã cho.

2.2 Định lý 2 (phép nhân, chia): Cho f(x) > g(x) xác định trên D

+ Nếu h(x) xác định trên D và h(x)>0 với mọi x \in D thì bất phương trình:

f(x) > g(x)<=> f(x).h(x) > g(x).h(x)

+ Nếu h(x) xác định trên D và h(x)<0 với mọi x \in D thì bất phương trình:

f(x) > g(x) <=> f(x).h(x) < g(x).h(x)

2.3. Định lí 3 (bình phương): Nếu f(x) > 0, g(x)>0 thì

f(x) > g(x) <=> {f^2}\left( x \right){\rm{ }} > {\rm{ }}{g^2}\left( x \right)

* Chú ý:  Khi giải bất phương trình  cần lưu ý các vấn đề sau

+ Đặt điều kiện (nếu có) trước khi biến đổi bất phương trình.

+ Khi nhân (chia) hai vế bất phương trình với một biểu thức thì chú ý xem biểu thức đó âm hay dương, hoặc biểu thức đó mang cả hai giá trị âm và dương.

+ Khi qui đồng mẫu số của bất phương trình: nếu biết chắc chắn mẫu dương thì không đổi dấu.

+ Nếu f(x)<0, g(x)<0 thì f(x)  -f(x) > -g(x). Khi đó ta có thể bình phương 2 vế.

* Ví dụ 1: Giải các bất phương trình sau

a) 2x+3 > x+7 <=> x > 4 => tập nghiệm là T = (4; + \infty )

b) 2x-10 > 3x-2<=> T = ( - \infty ; - 8] * Dấu của nhị thức bậc nhất

Định nghĩa: Nhị thức bậc nhất là biểu thức được biến đổi về dạng f(x) = ax+b ;  a \ne 0

* Dấu Tam thức bậc hai

Định nghĩa: Tam thức bậc hai là biểu thức có dạng f\left( x \right) = a{x^2} + bx + c;(a \ne 0).

 Phương pháp giải bất phương trình đại số 1 ấn

Phương pháp 1: Lập bảng

Ví dụ 1: Lập bảng xét dấu f(x)

a) f(x) = 2x - 3b)f\left( x \right){\rm{ }} = {\rm{ }}{x^2} - 4x - 5Giải

  1. f(x) = 0 \Leftrightarrow x = \frac{3}{2}

Dấu f(x)

Vậy: {f(x) > 0;\forall x \in \left( {\frac{3}{2}; + \infty } \right)} và {f(x) < 0;\forall x \in \left( { - \infty ;\frac{3}{2}} \right)}
b)cho f(x)= 0<=> {x_1} = - 1{\rm{ }};{x_2}{\rm{ }} = {\rm{ }}5 Dấu f(x) 

f(x) > 0;   \forall x \in ( - \infty ; - 1) \cup (5; + \infty )   và   f(x) < 0     \forall x \in ( - 1;5)

 

RELATED ARTICLESMORE FROM AUTHOR