Biến thiên trong toán học là gì? Các dạng biến thiên trong toán học

1. Biến thiên trong toán học là gì?

Thuật ngữ biến dùng để chỉ các đại lượng (chẳng hạn các đại lượng vật lý như khối lượng, thời gian, các đại lượng hình học như độ dài, diện tích, thể tích,…) có thể nhận các giá trị khác nhau trong một tập hợp nào đấy (được gọi là miền biến thiên của nó). Theo quan điểm động, người ta gọi chúng là các đại lượng biến thiên, hay đơn giản là các biến. Nếu tập hợp các giá trị của biến X là tập hợp số thì nó được gọi là biến số.

Cũng có những biến không phải là biến số như biến lôgic, biến Boolean, biến ký tự,… Giá trị của các biến thường liên quan đến nhau. Khi xét quan hệ giữa chúng với nhau, một số biến được xem là độc lập được gọi là các biến độc lập, một số biến sẽ nhận giá trị phụ thuộc vào các biến khác, được gọi là biến phụ thuộc. Xem thêm định nghĩa hàm số.

2. Các dạng biến thiên trong toán học?

Có 2 dạng biến thiên trong toán học chính đó là:

• Biến thiên trực tiếp (hoặc tỉ lệ thuận)
• Biến thiên ngược (hoặc tỉ lệ nghịch)

– Với biến thiên trực tiếp (Tỉ lệ thuận): Biến thiên trực tiếp xảy ra khi một đại lượng tăng lên thì đại lượng khác cũng tăng lên theo tỷ lệ nhất định. Ngược lại, nếu một đại lượng giảm, đại lượng kia cũng giảm.

Công thức:

• Nếu y tỉ lệ thuận với x, ta có thể viết: y=kx 
  Trong đó $k$ là hằng số tỉ lệ.

Ví dụ:

• Nếu một chiếc xe chạy với tốc độ không đổi, quãng đường $d$ mà xe đi được tỉ lệ thuận với thời gian $t$ mà xe chạy. Nếu tốc độ là v, ta có:
  d=vt

– Với biến thiên ngược (hoặc tỉ lệ nghịch): Biến thiên ngược xảy ra khi một đại lượng tăng lên thì đại lượng khác giảm đi, và ngược lại. Điều này có nghĩa là tích của hai đại lượng này luôn bằng một hằng số.

Công thức:

• Nếu y tỉ lệ nghịch với x, ta có thể viết:
  y=k/x​

  trong đó k là hằng số.

Ví dụ:

Nếu một công việc cần một số công nhân để hoàn thành trong một khoảng thời gian nhất định, thì số công nhân và thời gian làm việc có mối quan hệ tỉ lệ nghịch. Nếu số công nhân tăng, thời gian hoàn thành công việc sẽ giảm. Cụ thể, nếu một công việc cần k công nhân để hoàn thành trong $t$ giờ, thì:

với $n$ là số công nhân.

Ngoài 2 loại biến thiên là thuận và nghịch như mình đã giới thiệu ở trên ra thì còn một số loại biến thiên nhỏ hơn. Có thể kể đến như:

• Biến thiên bậc hai: Khi một đại lượng thay đổi theo bình phương của đại lượng khác. Ví dụ, diện tích hình vuông tỉ lệ thuận với bình phương cạnh của nó, hay A=a^2
• Biến thiên phi tuyến: Các mối quan hệ không phải là đường thẳng, mà có thể là đường cong. Ví dụ, hàm số bậc ba hoặc bậc bốn.

3. Ứng dụng của biến thiên:

– Kinh tế: Biến thiên giúp mô hình hóa mối quan hệ giữa cung và cầu. Nếu giá hàng hóa tăng (biến thiên trực tiếp), lượng cầu thường giảm (biến thiên ngược).

– Vật lý: Trong vật lý, nhiều hiện tượng tự nhiên có thể được mô tả bằng các mối quan hệ tỉ lệ. Ví dụ, trong định luật Hooke, lực đàn hồi tỉ lệ thuận với độ biến dạng của lò xo.

– Sinh học: Trong sinh học, biến thiên có thể mô tả sự thay đổi của quần thể theo thời gian, ảnh hưởng của môi trường đến sự sinh trưởng.

4. Đồ thị biến thiên trong toán học?

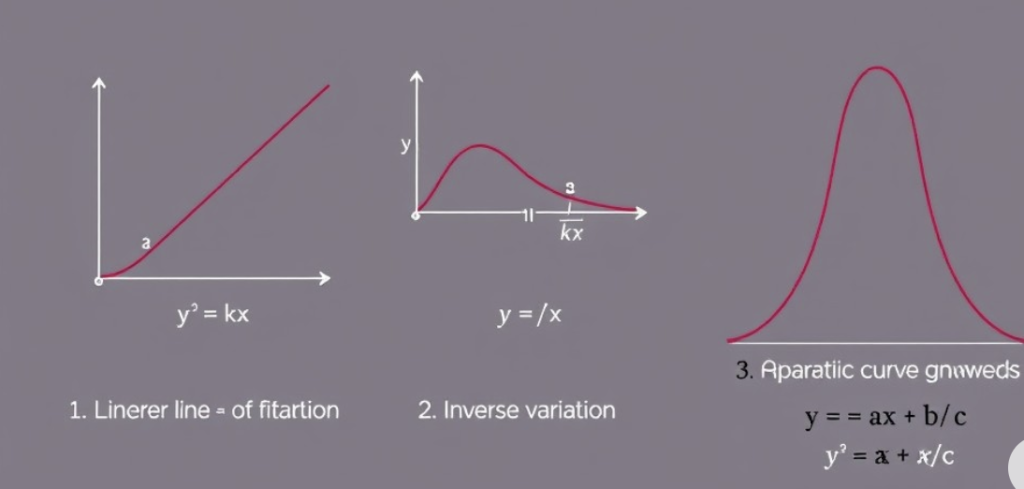
Ta có thể giải thích từng hình ảnh như sau:

– Biến Thiên Tuyến Tính (Linear Variation):

• Đồ Thị: Đường thẳng đi qua gốc tọa độ (0,0).
• Phương Trình: y=kx 
• Giải Thích: Trong biến thiên tuyến tính, giá trị của y thay đổi tỉ lệ với x. Hệ số k là độ dốc của đường thẳng. Nếu k>0, đường thẳng đi lên; nếu k<0 đường thẳng đi xuống.

– Biến Thiên Ngược (Inverse Variation):

• Đồ Thị: Đường cong hyperbol, tiến gần nhưng không chạm vào các trục tọa độ.
• Phương Trình: y=k/x​
• Giải Thích: Trong biến thiên ngược, khi $x$ tăng, $y$ giảm và ngược lại. Hệ số k là hằng số, và đồ thị có hai nhánh nằm ở các phần tư khác nhau của mặt phẳng tọa độ.

– Biến Thiên Bậc Hai (Quadratic Variation):

• Đồ Thị: Đường parabol mở lên.
• Phương Trình: y=ax^2+bx+c
• Giải Thích: Biến thiên bậc hai thể hiện mối quan hệ phi tuyến giữa y và x. Hệ số $a$ xác định hình dạng và hướng của parabol; nếu a>0 parabol mở lên; nếu a<0 parabol mở xuống.