1. Diện tích hình tam giác là gì?
* Hình Tam giác là gì?
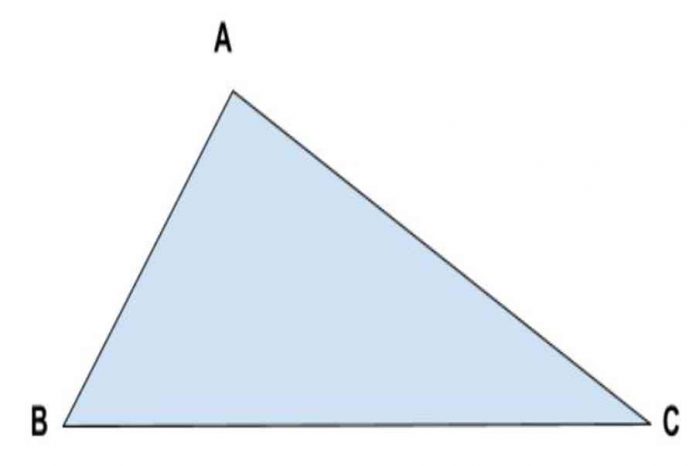
Hình tam giác là hình có ba đoạn thẳng nối các đỉnh với nhau và tổng ba góc trong một tam giác bằng 180 độ.
* Diện tích hình tam giác là gì?
Diện tích hình tam giác là tất cả phần mặt phẳng nằm bên trong hình tam giác đó.
2. Tam giác Thường và các công thức
Định nghĩa
Tam giác thường là tam giác có độ dài các cạnh và số đo góc trong khác nhau.
Công thức tính chu vi tam giác thường
Tam giác thường có chu vi bằng tổng độ dài của 3 cạnh.
P = a + b + c
Trong đó:
- P là chu vi của tam giác
- a, b, c lần lượt là 3 cạnh của hình tam giác đó.
Công thức tính diện tích tam giác thường:
Diện tích tam giác thường khi biết độ dài chiều cao sẽ được tính bằng ½ tích chiều cao hạ từ đỉnh nhân với chiều dài cạnh đáy đối diện của đỉnh tam giác đó.
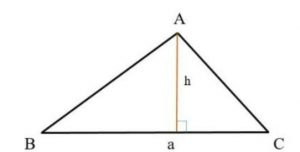
Công thức tính diện tích tam giác thường theo chiều cao:
S = ½ x a x h
Trong đó:
- a là Chiều dài cạnh đáy tam giác.
- h là Chiều cao được nối từ đỉnh và vuông góc với đáy của tam giác.
Ví dụ
Tính diện tích tam giác ABC có độ dài cạnh đáy BC là 12cm và chiều cao h là 5cm.
Lời giải:
Áp dụng công thức tính diện tích tam giác, ta có diện tích tam giác ABC là:
S = ½ x 12 x 5 = 30 (cm²).
3. Tam giác Vuông và các công thức
Định nghĩa
Tam giác vuông là tam giác có một góc vuông 90 độ.
Tính chất
- Tam giác có một góc vuông là tam giác vuông
- Tam giác có 2 góc nhọn phụ nhau là tam giác vuông
- Tam giác có đường trung tuyến ứng với 1 cạnh bằng nửa cạnh ấy là tam giác vuông.
- Tam giác có bình phương của 1 cạnh bằng tổng các bình phương 2 cạnh còn lại là tam giác vuông.
- Tam giác nội tiếp đường tròn có 1 cạnh là đường kính của đường tròn là tam giác vuông.
Công thức tính chu vi tam giác vuông
Chu vi tam giác vuông P = a + b + c
Trong đó:
A, b, c là độ dài 3 cạnh của tam giác
Công thức tính diện tích tam giác vuông
Trong tam giác vuông, nếu coi một cạnh góc vuông là đáy thì cạnh góc vuông còn lại là chiều cao. Diện tích tam giác bằng chiều dài đáy nhân với chiều cao tương ứng rồi chia 2.
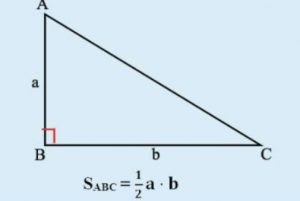
Hay:
Diện tích tam giác vuông bằng 1/2 tích của chiều cao với chiều dài đáy.
Công thức S = ½ x a x b
Trong đó:
+ a là Chiều cao của tam giác.
+ b là Cạnh đáy của tam giác.
Ví dụ
Tính diện tích hình tam giác vuông ABC với chiều cao là 20cm và độ dài cạnh đáy là 30 cm.
Lời giải:
Áp dụng công thức tính diện tích tam giác vuông, ta có diện tích tam giác vuông ABC là:
S = ½ x 20 x 30 = 300 (cm²).
4.Tam giác vuông cân và các công thức
Định nghĩa
Tam giác vuông cân là tam giác có hai cạnh vuông góc và bằng nhau.
Tính chất
- Tam giác vuông cân có 2 góc ở đáy bằng nhau và bằng 45 độ.
- Các đường cao, đường trung tuyến, đường phân giác kẻ từ đỉnh góc vuông của tam giác vuông cân trùng nhau và bằng nửa cạnh huyền.
Cụ thể:
Có tam giác ABC vuông cân tại A. Gọi D là trung điểm của BC. Thì, aD là đường cao đồng thời cũng là đường phân giác và là trung tuyến của BC.
AD = BD = DC = 1/2 BC.
Công thức tính diện tích tam giác vuông cân
Tam giác vuông cân là tam giác có một góc vuông, đồng thời thì chiều cao và cạnh đáy bằng nhau. Do vậy:
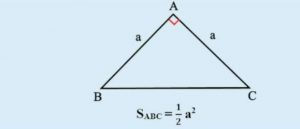
Diện tích tam giác vuông cân bằng ½ tích bình phương độ dài cạnh đáy hay cạnh góc vuông.
Công thức: S = ½ x a²
Trong đó, a là độ dài cạnh đáy của tam giác.
Ví dụ
Tính diện tích tam giác ABC vuông cân tại A, khi biết độ dài cạnh đáy AB là 8cm.
Lời giải:
Áp dụng công thức tính diện tích hình tam giác vuông cân, ta có diện tích tam giác ABC là:
S = ½ x 8² = 32 (cm²).
5. Tam giác Cân và các công thức
Định nghĩa
Tam giác cân là tam giác có 2 cạnh bằng nhau và số đo 2 góc ở đáy cũng bằng nhau.
Tính chất
- Trong tam giác cân có 2 cạnh bằng nhau và 2 góc ở đáy bằng nhau.
- Tam giác vuông cân là tam giác Vuông có 2 cạnh hay 2 góc ở đáy bằng nhau.
- Đường cao hạ từ đỉnh xuống đáy của tam giác cân cũng chính là đường trung tuyến và đường phân giác của tam giác đó.
Công thức tính Chu vi của tam giác cân
Chu vi của tam giác cân tương tự như tam giác thường.
P = a + b + c
Trong đó:
- P là Chu vi tam giác
- a, b, c lần lượt lag 3 cạnh của hình tam giác đó.
Công thức tính Diện Tích của tam giác Cân
Tam giác cân là tam giác có 2 cạnh bằng nhau. Hai cạnh này được gọi là hai cạnh bên và cạnh còn lại là cạnh đáy.
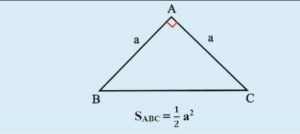
Diện tích tam giác cân cũng tương tự như diện tích tam giác thường bằng ½ tích của đường cao nối từ đỉnh nhân với cạnh đáy của tam giác đó.
Công thức: S = ½ x a x h
Trong đó:
- h: Chiều cao được nối từ đỉnh và vuông góc với đáy của tam giác.
- a: Chiều dài cạnh đáy tam giác.
Ví dụ
Cho tam giác ABC cân tại A, có đường cao bằng 12cm và độ dài cạnh đáy bằng 5cm. Tính diện tích tam giác cân ABC?
Lời giải:
Áp dụng công thức tính diện tích tam giác cân, ta có diện tích tam giác cân ABC là:
S = ½ x 12 x 5 = 30 (cm²).
6. Tam giác đều và các công thức liên quan
Định nghĩa
Tam giác đều là tam giác có 3 cạnh đều bằng nhau, 3 đường cao bằng nhau, 3 đường trung tuyến bằng nhau, 3 đường phân giác bằng nhau và ba góc bằng nhau đều bằng 60 độ.
Tính chất
- Nếu một tam giác có 3 góc bằng nhau thì tam giác đó là tam giác đều.
- Nếu một tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều.
- Trong tam giác đều, mỗi góc bằng 60 độ.
- Tam giác có 3 cạnh bằng nhau thì đó là tam giác đều
- Tam giác có 3 góc bằng nhau thì đó là tam giác đều
- Tam giác có 2 góc bằng 60 độ thì đó là tam giác đều.
Công thức tính chu vi tam giác đều
– Chu vi tam giác đều bằng 3 lần cạnh bất kỳ của tam giác.
Chu vi P = 3a
Trong đó:
- P là Chu vi tam giác đều
- a là chiều dài cạnh của tam giác.
Công thức tính diện tích tam giác đều
Diện tích tam giác đều bằng độ dài chiều cao nhân với cạnh đáy, được bao nhiêu chia cho 2.
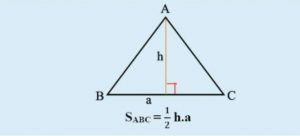
Công thức tính diện tích tam giác đều S = (a x h)/ 2.
Trong đó:
- a là chiều dài đáy của tam giác đều, đáy là một trong 3 cạnh của tam giác, cạnh đáy là cạnh nằm dưới cuối.
- h là chiều cao của tam giác, chiều cao này là đoạn thẳng hạ từ đỉnh xuống đáy của tam giác.
Ví dụ
Cho tam giác đều DEF, chiều cao bằng 8cm và độ dài cạnh đáy bằng 4cm. Tính diện tích tam giác đều DEF?
Lời giải:
Gọi h là chiều cao nối từ đỉnh D tới cạnh đáy EF và d là độ dài cạnh đáy EF.
Áp dụng công thức tính diện tích tam giác đều, ta có diện tích tam giác đều DEF là: S = ½ x 4 x 8 = 16 (cm²).
7. Kết luận:
Trên đây mình đã tổng hợp cho các bạn Công thức tính diện tích tam giác vuông? Ngoài ra còn có các công thức khác liên quan đến tính diện tích tam giác khác như:
- Diện tích tam giác đều
- Diện tích tam giác vuông
- Diện tích tam giác vuông cân
- Tính diện tích tam giác vuông
- Diện tích tam giác đều cạnh a
- Công thức tính diện tích tam giác vuông
- Công thức tính diện tích tam giác đều
- Cách tính diện tích tam giác vuông
- Diện tích hình tam giác vuông
- Công thức tam giác đều
- Tính diện tích tam giác đều
Chúc các bạn có các kiến thức bổ ích.