Tổng hợp các định lý trong toán học? Những định lý hay gặp trong các kì thi

Thực tế có rất nhiều các định lý trong toán học, và nếu còn đi học chúng ta thường sẽ chỉ sử dụng một số các định lý toán học tiêu biểu mà thôi.

1. Một số định lý hình học nổi tiếng 

Một số định lý Hình học nổi tiếng và áp dụng – tất cả có ở đây:

Download (PDF, 13.04MB)

Bao gồm:

• 1.2. Định lý Thales và định lý Pythagoras 
• 1.2.1. Định lý Thales 
• 1.2.2. Định lý Pythagoras 
• 1.3. Định lý hàm số sin và định lý hàm số cosin 
• 1.3.1. Định lý hàm số sin
• 1.3.2. Định lý hàm số cosin
• 1.4. Định lý Stewart và áp dụng
• 1.4.1. Định lý Stewart 
• 1.4.2. Định lý đường trung tuyến 
• 1.4.3. Định lý về đường phân giác
• 1.4.4. Công thức góc chia đôi 
• 1.5. Công thức về diện tích của tam giác và áp dụng 
• 1.5.1. Công thức về diện tích của tam giác 
• 1.5.2. Tỉ số diện tích hai tam giác
• 1.6.1. Pedal bất kỳ 
• 1.6.2. Pedal trực tâm
• Pedal tâm nội tiếp 
• 2.1. Ký hiệu và hệ thức cơ bản
• 2.2. Định lý Ptolemy và các mở rộng
• 2.2.1. Định lý Ptolemy 
• 2.2.2. Bất đẳng thức Ptolemy
• 2.2.3. Định lý Bretschneider 
• 2.2.4. Định lý Casey 
• 2.2.5. Định lý Carnot 
• 2.2.6. Bài toán
• 2.3. Tứ giác đặc biệt 
• 2.3.1. Tứ giác nội tiếp đường tròn
• 2.3.2. Tứ giác ngoại tiếp đường tròn .
• 2.3.3. Tứ giác đồng thời nội và ngoại tiếp 
• 2.3.4. Tứ giác với những đường chéo vuông góc
• 2.4. Công thức diện tích của tứ giác 
• 2.4.1. Công thức diện tích của tứ giác nội tiếp
• 2.4.2. Công thức diện tích của tứ giác ngoại tiếp 
• 2.5. Tứ giác điều hoà và tính chất 
• 2.5.1. Hàng điểm điều hoà .
• 2.5.2. Tứ giác điều hoà 
• 2.5.3. Tính chất của tứ giác điều hoà . 
• 3.1. Định lý Ceva
• 3.2.1. Định lý Ceva dạng sin 
• 3.2.2. Mở rộng định lý Ceva trong mặt phẳng
• 3.3. Mở rộng định lý Ceva trong không gian
• 3.3.1. Định lý Ceva trong không gian
• 3.3.2. Hệ quả của định lý Ceva trong không gian 
• 3.4. Các điểm đặc biệt trong tam giác 
• 3.4.1. Các điểm đặc biệt quen biết
• 4.1. Định lý Menelaus 
• 4.2. Mở rộng định lý Menelaus trong mặt phẳng
• 4.2.1. Mở rộng định lý Menelaus trong tam giác
• 4.2.2. Mở rộng định lý Menelaus theo diện tích
• 4.2.3. Mở rộng Định lý Menelaus trong tứ giác 
• 4.3. Mở rộng định lý Menelaus trong không gian 
• 4.3.1. Mặt phẳng phân giác góc nhị diện 
• 4.3.2. Định lý Menelaus trong không gian
• 4.4. Định lý Desargues và Định lý Pappus
• 4.4.1. Định lý Desargues 
• 4.4.2. Định lý Pappus 
• 4.5. Tam giác phối cảnh
• 5.1. Phương tích của một điểm – Trục đẳng phương 
• 5.1.1. Định lý về các dây cung cắt nhau
• 5.1.2. Phương tích của một điểm đối với một đường tròn
• 5.1.3. Trục đẳng phương và tâm đẳng phương 
• 5.2. Định lí Euler 
• 5.2.1. Đường thẳng Euler 
• 5.2.2. Đường tròn Euler
• 5.2.3. Công thức Euler 
• 5.3. Đường tròn Apolonius 
• 5.4. Định lí Simson 
• 5.5. Định lí Steiner 
• 5.5.1. Đường thẳng Steiner
• 5.5.2. Định lí Steiner 
• 5.6. Định lý Pithot 
• 5.7. Định lý Miquel 
• 5.8. Định lý Brianchon
• 5.9. Định lý Pascal và Định lý Newton
• 5.9.1. Định lý Pascal
• 5.9.2. Định lý Newton 
• 5.10. Định lý The’bault 

2. Một số định lý toán học lớp 10 phố biến?

Định lý Vi-ét:

Nếu phương trình bậc hai ax² + bx + c = 0 có hai nghiệm x₁; x₂ thì

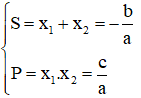
Định lí côsin:

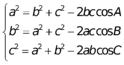
Định lí sin:

Công thức tính độ dài trung tuyến:

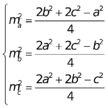
Định lý Py-ta-go

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

ΔABC vuông tại A ⇒ BC² = AB² + AC²