1. Volume trong toán học là gì?
Trong toán học, Volume hay còn được gọi là: “Thể tích” là một đại lượng toán học cho biết lượng không gian ba chiều chiếm bởi một vật thể hoặc một bề mặt khép kín. Đơn vị đo thể tích là đơn vị khối như m3 , cm , in3 v.v.
2. Định nghĩa:
Một Volume (thể tích) được định nghĩa đơn giản là lượng không gian bị chiếm bởi bất kỳ vật rắn ba chiều nào. Các chất rắn này có thể là hình lập phương, hình hộp chữ nhật, hình nón, hình trụ hoặc hình cầu.
Hình dạng khác nhau có khối lượng khác nhau. Trong hình học 3D, chúng ta đã nghiên cứu các hình dạng và chất rắn khác nhau như hình khối, hình lập phương, hình trụ, hình nón, hình chóp, v.v., được xác định trong không gian ba chiều. Đối với tất cả các hình này, chúng ta sẽ học cách tìm thể tích.
3. Đơn vị thể tích (volume)
Thể tích của vật rắn được đo bằng đơn vị khối. Ví dụ: nếu kích thước được tính bằng mét, thì thể tích sẽ tính bằng mét khối. Đây là đơn vị khối lượng tiêu chuẩn trong Hệ thống đơn vị quốc tế (SI). Tương tự, các đơn vị thể tích khác là centimet khối, feet khối, inch khối, v.v.
Ví dụ
Nếu một hình lập phương có kích thước 10cm x 3cm x 5cm, hãy tìm thể tích của nó.
Sol: Thể tích hình lập phương = dài x rộng x cao
V = 10cm x 3cm x 5cm
V = 150 phân khối
Do đó, chúng ta có thể thấy ở đây đơn vị thể tích của khối lập phương được đo bằng centimet khối.
4. Khối lượng (Volume) chất lỏng
Về cơ bản, thể tích của chất lỏng được đo bằng lít, trong đó 1 lít bằng 1000 cm3.
1 lít = 1000 phân khối = 0,001 mét khối
=> 1 mét khối = 1000 lít
Ngoài ra, để đo thể tích của một lượng nhỏ chất lỏng, chúng tôi sử dụng mililit.
1 mililit = 0,001 lít = 1 centimet khối
Thể tích chất lỏng cũng thường được đo bằng gallon.
1 lít = 0,264172 gallon chất lỏng Mỹ.
5. Công thức khối lượng (Volume)
Công thức tính thể tích của vật rắn trong không gian ba chiều là tìm tích các kích thước. Về cơ bản, thể tích bằng tích của diện tích và chiều cao của hình.
Khối lượng = Diện tích x Chiều cao
Đối với các hình có bề mặt phẳng như hình lập phương và hình lập phương, việc tìm thể tích rất dễ dàng. Nhưng đối với các hình dạng cong như hình nón, hình trụ và hình cầu, chúng ta cũng phải xem xét kích thước của bề mặt cong của chúng, chẳng hạn như bán kính hoặc đường kính.
4. Khối lượng (volume) của các hình khối
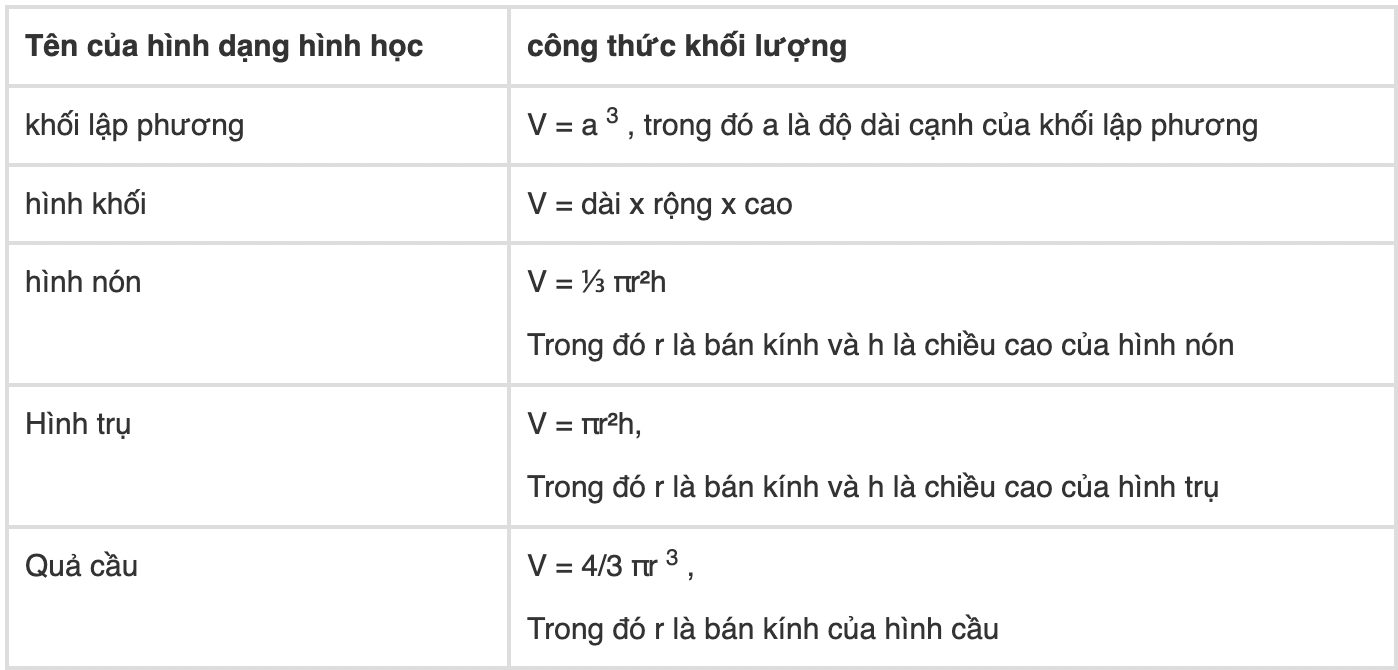
Khối lượng của các hình dạng khác:

5. Các ví dụ Volume
Câu 1: Tìm thể tích của hình lập phương biết độ dài cạnh của nó bằng 4 cm.
Giải: Cho chiều dài hình lập phương = 4cm
Như chúng ta biết,
Thể tích hình lập phương = Cạnh 3
Vì vậy,
Thể tích hình lập phương có chiều dài 4cm = 4 3 (cm) 3
Thể tích = 64 cm 3
Câu 2: Thể tích của hình nón là bao nhiêu nếu bán kính là 2cm và chiều cao là 5cm.
Giải: Cho bán kính đường tròn đáy của hình nón = 2cm
Chiều cao nón = 5cm
Như chúng ta biết,
Thể tích khối nón = ⅓ πr 2 h
Âm lượng = ⅓ π (2) 2 (5)
Âm lượng = ⅓ x 22/7 x 4 x 5
Khối lượng = 20,93 cu.cm.