Mặc dù từ “đồng vị” thường được người ta liên tưởng đến hóa học, trong toán học, nó cũng mang theo một ý nghĩa đặc biệt.
Trong hình học, đại số,… khái niệm về đồng vị và các khái niệm liên quan đóng một vai trò quan trọng trong việc nghiên cứu cấu trúc, biến đổi giữa các đối tượng toán học. Ở bài viết này hãy cùng mình khám phá về: “Đồng vị là gì trong toán học?” nhé.
1. Đồng vị là gì trong toán học?
– Đồng vị trong toán học:
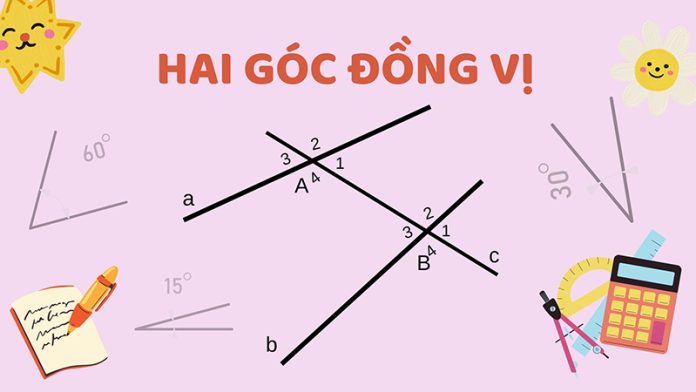
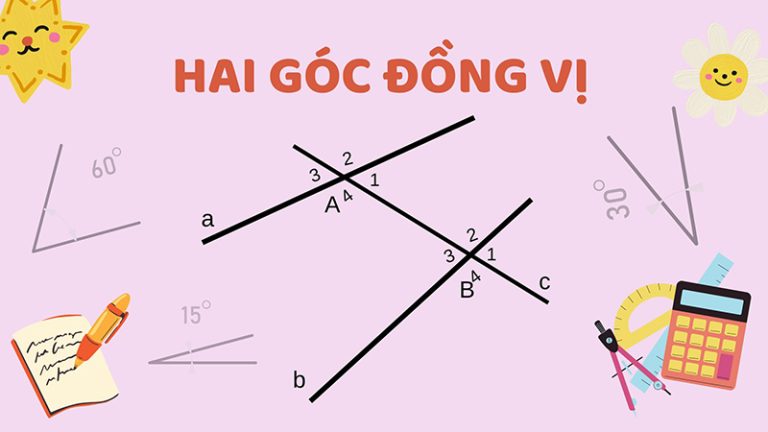
Trong toán học người ta hay nhắc nhiều về góc đồng vị hơn: Góc đồng vị là các cặp góc nằm ở vị trí tương ứng khi hai đường thẳng được cắt bởi một đường thẳng khác (đường cắt). Nếu hai đường thẳng song song và bị cắt bởi một đường thẳng khác, thì các góc đồng vị bằng nhau.
- Ví dụ: Nếu hai đường thẳng song song aa và bb bị cắt bởi đường thẳng cc, thì các góc ở cùng một phía của đường cắt và cùng một vị trí tương ứng trên hai đường song song được gọi là góc đồng vị.
2. Đồng vị trong hoá học?
– Đồng vị trong hoá học: Đồng vị của cùng một nguyên tố hoá học là những nguyên tử có cùng số proton nhưng khác nhau về số nơtron, do đó số khối A của chúng khác nhau.
Ví dụ:
- Nguyên tố clo có hai đồng vị bền là:
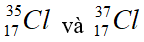
- Nguyên tố hiđro có ba đồng vị là
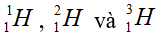
- Nguyên tố đồng có hai đồng vị bền là
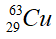và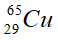 
.
3. Các tính chất khác của góc đồng vị?
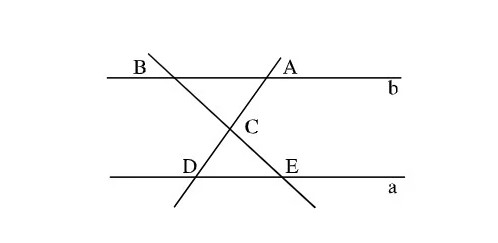
- Góc so le trong (Alternate Interior Angles): Khi hai đường thẳng bị cắt bởi một đường thẳng khác, các cặp góc nằm ở bên trong của hai đường thẳng đó và ở hai phía đối diện của đường cắt gọi là góc so le trong. Nếu hai đường thẳng là song song, các góc so le trong cũng bằng nhau.
- Góc trong cùng phía (Consecutive Interior Angles): Các góc nằm ở cùng một phía của đường cắt và nằm bên trong hai đường thẳng được gọi là góc trong cùng phía. Nếu hai đường thẳng là song song, tổng của các góc này sẽ bằng 180 độ.
- Khi hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba, các góc đồng vị luôn luôn bằng nhau.
- Góc đồng vị là những góc nằm ở vị trí giống nhau ở hai đường thẳng song song.
- Nếu một đường thẳng cắt hai đường thẳng song song thì sẽ có 4 cặp góc đồng vị với nhau.
Quan hệ giữa các cặp góc: Nếu hai đường thẳng cắt một đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
– Hai góc so le trong còn lại bằng nhau
– Hai góc đồng vị bằng nhau
– Hai góc trong cùng phía bù nhau
4. Các Bài tập ví dụ về góc đồng vị và cách giải?
– Nhận biết hai góc đồng vị: Phương pháp giải: Dựa vào khái niệm góc đồng vị
– Tính số đo của các góc tạo thành từ một đường thẳng cắt hai đường thẳng
– Áp dụng tính chất về hai góc đồng vị, hai góc kề bù, hai góc đối đỉnh và dựa vào yêu cầu bài toán để phân tích, suy luận tìm ra phương pháp giải thích hợp nhất
– Bài tập có kiến thức tổng hợp liên quan đến hai góc đồng vị: Phương pháp giải: Tùy vào yêu cầu của bài toán để phân tích, suy luận đưa ra phương pháp giải chính xác và thích hợp nhất.
Để chứng minh rằng hai góc là đồng vị, ta cần chứng minh rằng chúng có cùng độ lớn và cùng đỉnh.
Có thể sử dụng các phương pháp sau để chứng minh điều này:
– Sử dụng định nghĩa: Hai góc được gọi là đồng vị nếu chúng có cùng độ lớn và cùng đỉnh. Vì vậy, để chứng minh rằng hai góc đồng vị, ta chỉ cần chứng minh rằng chúng có cùng độ lớn và cùng đỉnh.
– Sử dụng đẳng thức góc: Để chứng minh rằng hai góc đồng vị, ta có thể sử dụng đẳng thức góc để so sánh chúng. Điều này đòi hỏi ta phải chuyển đổi các góc về cùng đơn vị đo và so sánh chúng.
– Sử dụng các phép biến đổi hình học: Ta có thể sử dụng các phép biến đổi hình học như quay, dịch và phóng để chuyển đổi các góc để chúng trở thành các góc đồng dạng với nhau. Sau đó, ta có thể so sánh chúng để chứng minh rằng chúng đồng vị.
– Sử dụng các định lí hình học: Có nhiều định lí trong hình học có thể được sử dụng để chứng minh rằng các góc đồng vị. Ví dụ, định lí góc bù, định lí góc đối, định lí Euclid về góc, và định lí hai góc bằng nhau (HL) là một số trong số những định lí này.
4. Kết luận:
Trên đây là bài viết của mình về “Đồng vị là gì trong toán học? Tìm hiểu ý nghĩa?” – chúc các bạn có các kiến thức thú vị.
