1. Gradient trong toán học là gì?
Gradient (độ dốc) là khái niệm rất gần với khái niệm đạo hàm mà chúng ta đã học thời cấp 3, nó biểu diễn cho tốc độ thay đổi của hàm. Gradient là một vectơ trong khi đạo hàm là giá trị vô hướng (hiểu nôm na là các giá trị số). Véc tơ này chỉ ra hướng mà tại đó giá trị của hàm thay đổi nhiều nhất và trở thành véc tơ 0 khi hàm đạt giá trị cực đại hoặc cực tiểu địa phương.
2. Biểu diễn toán học của Gradient
Gradient của một hàm f(x1,x2,…,xn), được ký hiệu ∇f là một vector n chiều, mà mỗi thành phần trong vector đó là một đạo hàm riêng phần (partial derivative) theo từng biến của hàm đó:

3. Ứng dụng của Gradient trong toán học?
Gradient trong toán học có các ứng dụng sau:
- Tối Ưu Hóa: Dùng để xác định hướng và độ lớn của sự thay đổi nhanh chóng của một hàm số, đặc biệt trong thuật toán tối ưu hóa như gradient descent.
- Machine Learning: Sử dụng để cập nhật trọng số của mô hình, giúp mô hình học từ dữ liệu và tối ưu hóa hiệu suất dự đoán.
- Đại Số Đạo Hàm: Được sử dụng để xác định đạo hàm riêng của hàm nhiều biến.
- Phương Trình Đạo Hàm Bất Định: Giúp xác định phương trình đạo hàm bất định của một hàm.
- Hình Học Tích Phân: Dùng để xác định hướng của đường tiếp tuyến tại một điểm trên đồ thị của một hàm số.
- Phương Trình Đạo Hàm Riêng (PDE): Được sử dụng để giải phương trình đạo hàm riêng.
- Xác Định Điểm Cực Tiểu và Cực Đại: Được sử dụng để xác định vị trí các điểm cực tiểu và cực đại của một hàm số.
- Phân Loại và Clustering: Sử dụng để điều chỉnh trọng số mô hình trong các bài toán phân loại và nhóm.
4. Gradient trong các mảng khác là gì?
Thông thường trong các mảng khác sử dụng nhiều nhất có lẽ phải kể đến photoshop? Đây là hình ảnh cho bạn dễ hình dung?
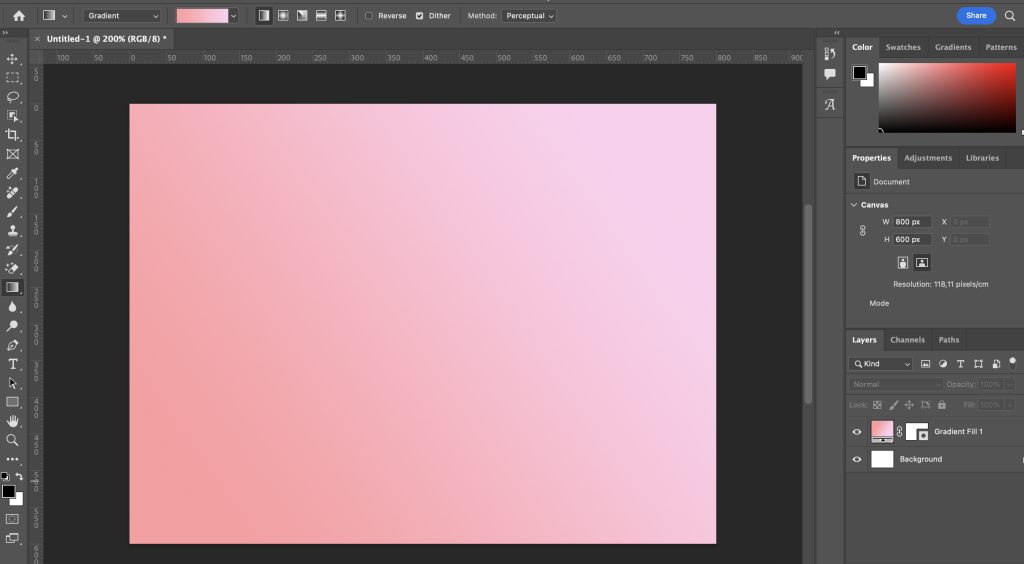
Trên là hình ảnh màu Gradient trong photoshop – cụ thể Gradient từ “Gradient” thường được hiểu là “độ chuyển đổi màu sắc” hoặc “độ chuyển đổi đồng tuyến từ một màu sang một màu khác”.
5. Kết luận?
Trên đây mình đã tổng hợp cho các bạn về gradient trong toán học nghĩa là gì? thậm chí là gradient là gì trong photoshop nữa. Hi vọng với các kiến thức mình tổng hợp cho các bạn – các bạn sẽ có các kiến thức thú vị






















[…] Gradient trong toán học nghĩa là gì? […]
[…] Gradient trong toán học nghĩa là gì? […]
Comments are closed.