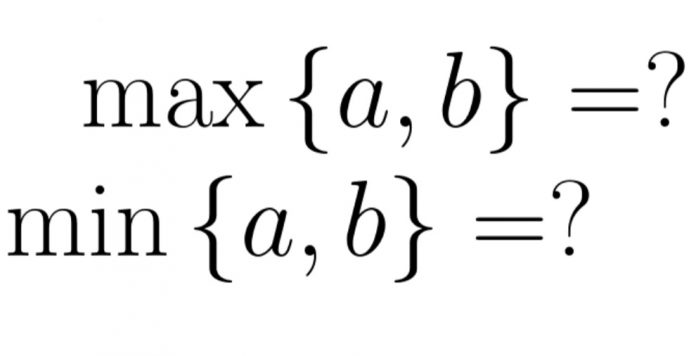Nếu học toán học chúng ta sẽ không lạ gì với khái niệm Min và max trong toán học. Bài viết này hãy cùng sieutonghop sẽ nêu lại khái niệm Max và Min trong toán học.
1. Max trong toán học là gì?
Để dễ hiểu thì: MAX là GTLN của biểu thức.
2. Min trong toán học là gì?
Để dễ hiểu thì: Min là GTNN của biểu thức.
3. Ví dụ về bài toán max min trong toán học?
Ví dụ 1: Giá trị lớn nhất của hàm số f(x) = x3 – 8x2 + 16x – 9 trên đoạn [1; 3] là:
Nhận xét: Hàm số f(x) liên tục trên [1;3]
Ta có đạo hàm y’= 3×2 – 16x + 16

Do đó :

Suy ra ta chọn đáp án B.
Ví dụ 2: Giá trị lớn nhất của hàm số f(x) = x4 – 2x2 + 1 trên đoạn [0; 2] là:

Nhận xét: Hàm số f(x) liên tục trên [0;2]
Ta có y’ = 4x3 – 4x = 4x(x2 – 1).
Xét trên (0;2) ta có f'(x) = 0 khi x = 1.
Khi đó f(1) = 0; f(0) = 1; f(2)= 9
Do đó 
Suy ra chọn đáp án D.
Ví dụ 3: Giá trị nhỏ nhất của hàm số y = x(x + 2).(x + 4).(x + 6) + 5 trên nữa khoảng [-4; +∞) là:

Nhận xét: Hàm số f(x) liên tục trên
* Ta có: y = (x2 + 6x).(x2 + 6x + 8) + 5.
Đặt t = x2 + 6x. Khi đó y = t.(t + 8) + 5 = t2 + 8t + 5
* Xét hàm số g(x)= x2 + 6x với x ≥ -4.
Ta có g'(x) = 2x + 6; g'(x) = 0 khi và chỉ khi x = -3

Bảng biến thiên:

Suy ra t ∈ [-9; +∞)
* Yêu cầu bài toán trở thành tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y = h(t)= t2 + 8t + 5 với t ∈ [-9; +∞).
* Ta có h'(t) = 2t + 8
h'(t) = 0 khi t = – 4; 
Bảng biến thiên

Vậy 
Suy ra chọn đáp án B. (Tham khảo nguồn kienguru.vn)