Định nghĩa hình chóp đều là gì? Các loại hình chóp thường gặp

1. Hình chóp đều là gì?

Hình chóp đều là hình chóp thoả 2 điều kiện sau:

• Đáy là đa giác đều (tam giác đều, hình vuông, …)
• Chân đường cao của hình chóp là tâm của đáy

Từ định nghĩa suy ra hình chóp đều có các cạnh bên bằng nhau.

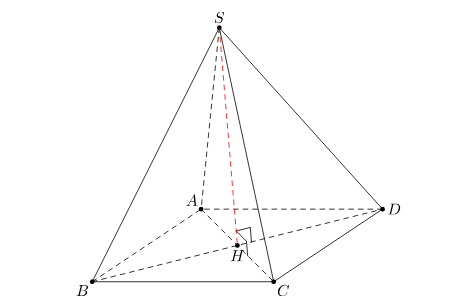
Hình chóp đều 𝑆.𝐴𝐵𝐶𝐷 có: 𝐴𝐵𝐶𝐷 là hình vuông, 𝐻 là giao điểm của hai đường chéo thì 𝑆𝐻⊥(𝐴𝐵𝐶𝐷)

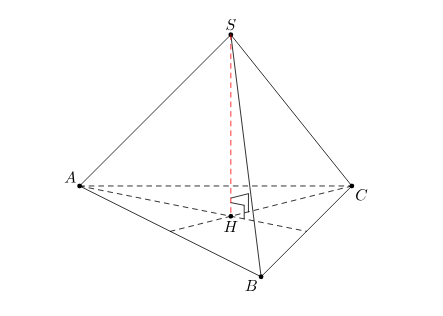
Hình chóp đều 𝑆.𝐴𝐵𝐶 có: 𝐴𝐵𝐶 là tam giác đều, 𝐻 là giao điểm của 3 đường trung tuyến thì 𝑆𝐻⊥(𝐴𝐵𝐶).

Chú ý:

• Tâm của tam giác đều là giao điểm 3 đường trung tuyến, cũng là đường cao, trung trực, phân giác trong
• Tâm của hình vuông là giao điểm hai đường chéo của nó

Thuật ngữ

• Hình chóp tam giác đều là hình chóp đều có đáy là tam giác
• Hình chóp tứ giác đều là hình chóp đều có đáy là tứ giác

2. Công thức tính thể tích của hình chóp tứ giác đều

Để tính được thể tích của hình chóp tứ giác đều thì ta cần phải biết được các công thức sau:

• Diện tích hình vuông: S = cạnh²
• Đường chéo hình vuông: cạnh x căn bậc 2
• Thể tích hình chóp tức giác SABCD:
  

Thể tích của hình chóp được tính bằng một phần ba tích của chiều cao và diện tích mặt đáy (nghĩa là bằng một phần ba thể tích của hình lăng trụ có chung đáy và chiều cao với hình chóp). Có sự tương đồng giữa công thức này với công thức diện tích tam giác (nửa tích chiều cao và cạnh đáy) khi mở rộng từ không gian hai chiều lên ba chiều.

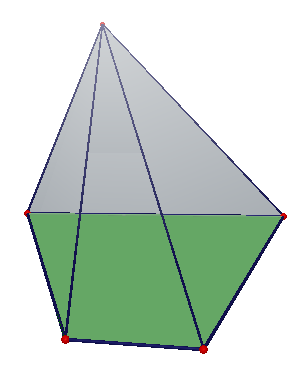
3. Hình chóp đa giác đều là gì?

Hình chóp đa giác đều là hình chóp có đáy là đa giác đều và chân đường vuông góc hạ từ đỉnh xuống mặt phẳng đáy trùng với tâm của đa giác đáy.
– Hình chóp đều là hình chóp có đáy là đa giác đều, các cạnh bên bằng nhau và bằng cạnh của đa giác đáy.
– Các mặt bên của chóp đa giác đều là các tam giác cân, bằng nhau.
– Các mặt bên của chóp đều là các tam giác đều.

– Lăng trụ bạn có thể hiểu là đa diện có hai mặt (đáy) song song với nhau, còn các mặt còn lại (các mặt bên) đều là những hình bình hành.
– Nếu các mặt bên (hoặc các cạnh bên) của lăng trụ vuông góc với mặt đáy thì lăng trụ đó gọi là lăng trụ đứng.
– Lăng trụ đứng có đa giác đáy là đa giác đều thì gọi là lăng trụ đều.
– Các cạnh bên của lăng trụ bằng nhau. Các mặt bên của lăng trụ đều là hình bình hành. Các mặt bên của lăng trụ đứng là hình chữ nhật. Các mặt bên của lăng trụ đều là các hình chữ nhật bằng nhau.
– Trong trường hợp lăng trụ đứng hoặc đều thì độ dài đường cao bằng độ dài cạnh bên.
– Lăng trụ bất kì thì độ dài đường cao băng độ dài cạnh bên nhân cos góc giữa cạnh bên với mặt đáy