1. Chuỗi trong toán học là gì?
Trong toán học, chuỗi có thể được nói là, việc cộng lại vô hạn các số lại với nhau bất đầu từ số ban đầu. Chuỗi là phần quan trọng của vi tích phân và trong tổng quát của nhánh đó, giải tích toán học. Chuỗi được sử dụng trong đa số các nhánh toán học, kể cả cho việc nghiên cứu các cấu trúc hữu hạn (ví dụ như trong tổ hợp) qua các hàm sinh.
Ngoài sự phổ biến của nó trong toán học ra, chuỗi vô hạn cũng được sử dụng rộng rãi trong các môn khoa học khác như vật lý, khoa học máy tính, thống kê và kinh tế học.
2. Các tính chất cơ bản của chuỗi trong toán học?
Chuỗi vô hạn hay gọi ngắn đi là chuỗi là tổng vô hạn được biểu diễn bằng biểu thức sau:[3]
Trong đó 
là bất kỳ dãy được sắp của các số hạng, như là các số, hàm số, hay bất cứ thứ gì có thể cộng với nhau (trong nhóm abel). Đây là biểu thức lấy được từ dãy bằng cách đặt các số hạng cạnh nhau rồi nói chúng bằng ký hiệu phép cộng “+”. Chuỗi có thể viết gọn lại bằng ký hiệu sigma thành
Nếu nhóm abel A của các số hạng có khái niệm giới hạn (tức là nó là không gian mêtric), thì một số chuỗi có thể có giá trị trong A, giá trị đó được gọi là tổng của chuỗi. Định nghĩa này có bao gồm cả các trường hợp thường gặp trong giải tích, trong đó nhóm là trường số thực hoặc trường số phức. Cho chuỗi {\textstyle s=\sum _{n=0}^{\infty }a_{n}}, tổng riêng thứ k của nó là
Theo định nghĩa, chuỗi hội tụ đến giá trị L (hay có tổng bằng L), nếu dãy các tổng riêng của nó có giới hạn L. Khi đó, ta thường viết là
Một chuỗi được gọi là hội tụ nếu nó hội tụ đến một giá trị hữu hạn nào đó, hay phân kỳ nếu nó không hội tụ được. Giá trị của giới hạn này, nếu nó tồn tại, là giá trị của chuỗi.
* Chuỗi Σan
Được gọi là hội tụ khi dãy (sk) của các tổng riêng có giới hạn. Nếu giới hạn của sk là vô cực hay không tồn tại, thì chuỗi được gọi là phân kỳ. Khi giá trị hữu hạn của giới hạn tồn tại, nó được gọi là giá trị (hay tổng) của chuỗi.
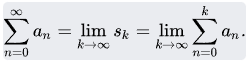
Cách dễ nhất để một chuỗi vô hạn hội tụ là khi an bằng không với mọi n đủ lớn. Dễ thấy một chuỗi số như vậy có thể được viết dưới dạng một tổng hữu hạn, cho nên chuyện dãy số đó là vô hạn không có ý nghĩa gì.
Tìm ra các giá trị của một chuỗi hội tụ kể cả khi tất cả các biểu thức đều khác không là tiêu điểm của việc nghiên cứu chuỗi. Xem xét ví dụ sau:
Có thể “hình dung”sự hội tụ của chuỗi trên trục số thực: ta có thể hình dung một đoạn thẳng có chiều dài bằng 2, trên đó lần lượt bôi đen các phần với chiều dài 1, ½, ¼, v.v. Luôn luôn còn chỗ để bôi đen phần tiếp theo vì phần đoạn thẳng còn lại luôn luôn bằng phần đoạn thẳng vừa đánh dấu. Thật vậy, khi ta đã bôi đen ½, ta vẫn còn một phần có chiều dài ½ chưa bị bôi đen, nên hoàn toàn có thể bôi đen tiếp ¼, và cứ như thế. Điều này không chứng minh rằng tổng này bằng 2 (mặc dù đúng là như thế), nhưng nó chứng minh rằng tổng này nhỏ hơn hoặc bằng 2. Nói cách khác, giá trị chuỗi này có cận trên. Biết rằng chuỗi này hội tụ, để chứng minh nó có giá trị bằng 2, ta chỉ cần đại số cơ bản. Nếu chuỗi được ký hiệu là S, dễ thấy rằng:
Do đó,
Các nhà toán học có thể mở rộng từ ví dụ này để thể hiện các khái niệm khác, tương đương của chuỗi. Ví dụ, khi ta nói về số thực có lặp phần thập phân, chẳng hạn: {\displaystyle x=0.111\dots } thực ra ta đang nói về chuỗi số mà nó thể hiện (0.1 + 0.01 + 0.001 + …). Tuy nhiên, vì những chuỗi này luôn hội tụ về số thực (bởi tính đầy đủ của số thực), nên nói về chuỗi số theo cách này cũng giống như nói về các số mà chúng thể hiện. Đặc biệt, không nên thấy bất hợp lý khi coi 0.111… và 1/9 là một. Lập luận rằng 9 × 0.111… = 0.999… = 1 không hiển nhiên, nhưng hoàn toàn chứng minh được một khi đã biết các định luật về giới hạn bảo toàn các phép tính số học.
