1. Phép chia gọi là gì?
Trong toán học phép chia thường được biểu diễn trong đại số và khoa học bằng cách đặt số bị chia trên số chia với một dòng kẻ ngang đặt giữa chúng, còn được gọi là vinculum hay thanh phân số. Ví dụ, a chia b được viết là:
![]()
Có thể đọc là “a bị chia bởi b”, “a chia b”, “a trên b” hay “a phần b”. Một cách để biểu diễn phép chia trên cùng một dòng là viết số bị chia (còn gọi là tử số), rồi gạch chéo, rồi số chia (còn gọi là mẫu số) như sau:
Đây là cách thông thường để biểu diễn phép chia trong hầu hết ngôn ngữ lập trình của máy tính bởi vì nó có thể dễ dàng gõ thành một loạt các ký tự với bảng mã ASCII.
Trong bản in, người ta còn sử dụng một dạng biểu diễn giữa hai cách này, đó là sử dụng dấu gạch chéo nhưng viết số bị chia lên trên và số chia ở dưới:
- a⁄b
Bất kỳ dạng nào ở trên đều có thể sử dụng để biểu diễn một phân số. Phân số là một dạng biểu diễn phép chia trong đó số bị chia (mẫu số) và số chia (tử số) đều là số nguyên.
Ngoài ra, một cách thông thường trong số học (không dùng dạng phân số) để thể hiện phép chia là sử dụng dấu ôben (dấu chia), ví dụ như:
=> Nguyên tắc:
a:b = c
Trong đó:
- a là số chia
- b là số bị chia
- Kết quả của phép chia là “c” tức là thương
2. Ví dụ về phép chia:
– Phép chia không dư
Ví dụ: 127: 4
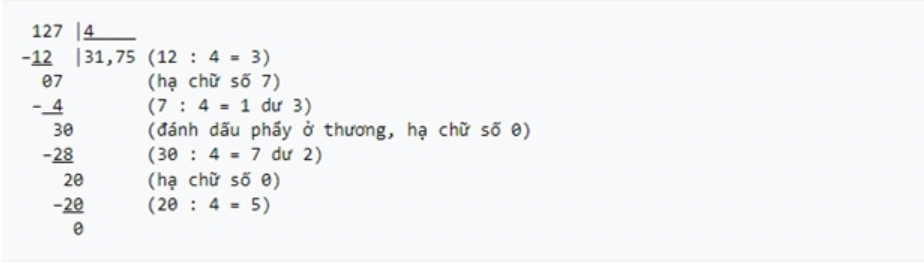
Cách tính được trình bày như sau:
- Lấy (bộ) số ngắn nhất đầu tiên trong số bị chia mà chia được cho số chia. Ở đây vì 1 không chia được 4 nên ta lấy 12 chia 4 được 3; 3 nhân 4 bằng 12; 12 trừ 12 còn 0.
- Hạ chữ số tiếp theo xuống. Ở đây ta hạ 7; 7 chia 4 được 1; 1 nhân 4 bằng 4; 7 trừ 4 còn 3.
- Nếu chia hết phần số nguyên mà muốn chia tiếp, ta phải đánh dấu thập phân ở thương số và hạ một số 0 ở phần chia. Ở đây ta hạ 0; 30 chia 4 được 7; 7 nhân 4 bằng 28; 30 trừ 28 còn 2.
- Hạ tiếp một số 0; 20 chia 4 được 5; 5 nhân 4 bằng 20; 20 trừ 20 còn 0. Kết quả là 31,75.
– Phép chia có dư:
Cho hai số tự nhiên a và b, trong đó b khác 0. Ta luôn tìm được đúng hai số tự nhiên q và r sao cho :
a = b.q + r ( trong đó, 0 ≤ r < b)
- Ta gọi q và r lần lượt là thương và số dư trong phép chia hết a : b = q
- Nếu r khác 0 thì ta nói a không chia hết cho b. Và từ đó, ta có khái niệm về phép chia có dư.
- Kí hiệu: a ⋮̸ b
Ví dụ: 7: 2
Nếu a = 7 và d = 2, khi đó q = 3 và r = 1, vì 7 = (2)(3) + 1.

3. Một số tính chất của phép chia:
- Tính duy nhất của kết quả: Với mọi số nguyên và (với a≠0), tồn tại một số nguyên duy nhất sao cho .
- Tính chia hết: Nếu chia hết cho (a mod b=0), thì tồn tại một số nguyên sao cho .
- Số dư: Nếu và là hai số nguyên, tồn tại một số nguyên và một số nguyên dư sao cho a, với .
- Chia cho 0: Phép chia cho 0 không xác định. Trong toán học, không thể chia một số cho 0.
- Quy tắc dấu: Khi chia hai số cùng dấu, kết quả là dương. Khi chia hai số khác dấu, kết quả là âm.
- Luật kết hợp:

- Luật nhân với nghịch đảo:

- Phép chia với số 1:

- Phép chia số 0 cho một số khác 0: Phép chia cho 0 là không xác định
- Phép chia cho số 0: Nếu a≠, thì a/b là vô cùng dương hoặc vô cùng âm, tùy thuộc vào dấu của .
4. Kết luận:
OK vậy là bài viết trên đây mình đã giới thiệu cho mọi người về Phép chia trong toán học gọi là gì? cùng với đó là các ví dụ và các tính chất của phép chia. Chúc các bạn thành công





















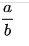









[…] >>> Phép chia trong toán học […]
Comments are closed.