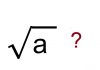Trong tiếng Anh, “Root” có nghĩa gốc là cái rễ cây. Trong toán học, người ta mượn hình ảnh này để ám chỉ một thứ gì đó là “nguồn gốc”, là “nền tảng” sinh ra những thứ khác, hoặc là “điểm gốc” nơi mọi thứ bắt đầu.
Tùy vào việc bạn đang làm toán Số, toán Đại số hay Hình học, “Root” sẽ có 3 khuôn mặt chính. Sieutonghop.com sẽ hướng dẫn cho các bạn nhé.
1. Root là gì trong toán học?
Trong toán học, “root” (căn) có thể là một giá trị mà khi lũy thừa với một số mũ nhất định sẽ cho ra một số đã cho. Một nghĩa khác của “root” là nghiệm của một phương trình, tức là giá trị của biến làm cho phương trình có giá trị bằng 0.
“Căn” cũng có thể chỉ căn bậc hai, là phép toán nghịch đảo của phép bình phương, hoặc căn bậc n nói chung.
2. Các Root trong toán học?
* Root trong Số học (Arithmetic): Phép khai căn
Trong ngữ cảnh này, “root” đề cập đến một con số mà khi được lũy thừa lên (nhân với chính nó), sẽ tạo ra con số ban đầu. Đây là khái niệm phổ biến nhất mà chúng ta thường gặp.
- Căn bậc hai (Square Root): Là số x sao cho khi nhân nó với chính nó (x²) sẽ bằng số đã cho.
Ví dụ: Căn bậc hai của 9 là 3, vì 3 × 3 = 9. (Ký hiệu: √9 = 3).
- Căn bậc n (n-th Root): Khái niệm mở rộng. Căn bậc n của một số là giá trị mà khi được nhân với chính nó n lần sẽ ra số ban đầu.
Ví dụ: Căn bậc 3 (Cube root) của 8 là 2, vì 2 × 2 × 2 = 8.
- Liên hệ với số mũ: Trong toán cao cấp, phép lấy căn thực chất là lũy thừa với số mũ phân số. Ví dụ: Căn bậc hai của x chính là x mũ 1/2 (x1/2).
⚠️ Lưu ý quan trọng về dấu: Một số dương thực tế có hai căn bậc hai (một dương và một âm). Ví dụ: 3 bình phương bằng 9, và -3 bình phương cũng bằng 9. Tuy nhiên, ký hiệu căn toán học (√) quy ước chỉ lấy giá trị dương (gọi là căn số học).
* Root của phương trình (Equation Root): Nghiệm
Root của một phương trình (ví dụ f(x)) là giá trị của biến số x làm cho phương trình đó có kết quả bằng 0. Do đó, người ta còn gọi nghiệm là “Zeros of the polynomial” (Điểm 0 của đa thức).
Ví dụ minh họa:
- Cho phương trình: f(x) = x – 2
- Để tìm root, ta đặt: x – 2 = 0
- Suy ra: x = 2. Vậy 2 là một nghiệm (root), vì f(2) = 2 – 2 = 0.
Ý nghĩa trên đồ thị (Hình học):
Nếu vẽ hàm số lên hệ trục tọa độ, “Root” chính là hoành độ giao điểm giữa đường đồ thị và trục hoành (trục ngang x-axis). Tại điểm cắt này, giá trị y luôn bằng 0.
* Root trong Lý thuyết đồ thị & Khoa học máy tính
Đây là nghĩa ít gặp trong toán phổ thông nhưng rất quan trọng trong Tin học (Cấu trúc dữ liệu cây – Tree).
- Root (Nút gốc): Là nút (node) nằm ở vị trí cao nhất, đầu tiên của một cây dữ liệu.
- Đặc điểm: Tất cả các nhánh và nút con đều phát triển từ Root này. Nó là nút duy nhất trong cây không có nút cha (parent).
3. Cuối cùng?
Nêuus bạn thích tìm hiểu thêm thì: Từ “Root” xuất phát từ tiếng Latin là radix (nghĩa là rễ cây). Các nhà toán học xưa quan niệm rằng:
- Kết quả của một phương trình hay một con số lớn giống như cái cây mọc trên mặt đất (phần nhìn thấy).
- Giá trị nghiệm (x) hay căn số là cái gốc rễ nằm ẩn bên dưới, là nguồn gốc tạo nên cái cây đó.
| Ngữ cảnh | Ý nghĩa của Root | Ví dụ |
|---|---|---|
| Số học | Phép khai căn (ngược với lũy thừa) | √16 = 4 |
| Đại số | Giá trị x làm phương trình bằng 0 (Nghiệm) | x² – 9 = 0 → x = 3 |
| Hình học | Giao điểm với trục hoành (x-axis) | Điểm cắt trục ngang |
| Tin học | Nút khởi đầu (Nút gốc) | Thư mục gốc (Root directory) |