1. Span trong toán học?
Trong toán học, span tuyến tính (hay bao tuyến tính hay gọi tắt là span) của một tập hợp vectơ S (từ một không gian vectơ), ký hiệu span(S), là không gian con tuyến tính nhỏ nhất chứa tập hợp vectơ đó. … Khái niệm span có thể được tổng quát hóa cho matroid và mô đun.
Để diễn đạt rằng không gian vectơ V là span của tập hợp vectơ S, ta còn có thể nói: S span V; S sinh ra V; V được span bởi S; V được sinh bởi S; S là một hệ sinh của V; hay S là hệ span của V.
2. Công thức Span?
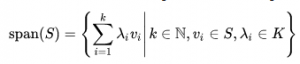
Trong trường hợp nếu S là một tập hợp con hữu hạn trong V thì span của S là tập hợp tất cả các tổ hợp tuyến tính của các phần tử trong S. Trong trường hợp tập hợp S là vô hạn, các tổ hợp tuyến tính vô hạn (tức là các tổ hợp có thể liên quan đến một tổng vô hạn, và giả thiết rằng các tổng trên được xác định theo một cách nào đó, chẳng hạn như trong không gian Banach) thì định nghĩa trên không áp dụng được; còn tổng quát hóa có thể áp dụng được với chúng thì lại không tương đương.