1. Phương trình đường tròn là gì?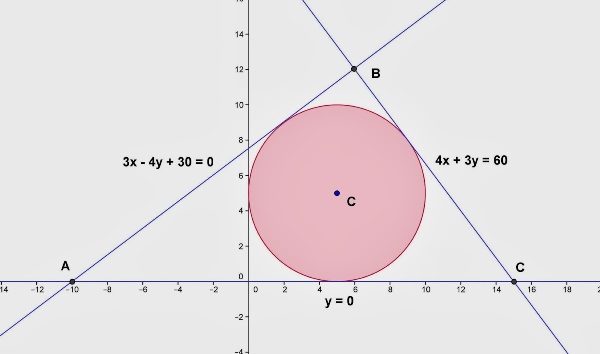
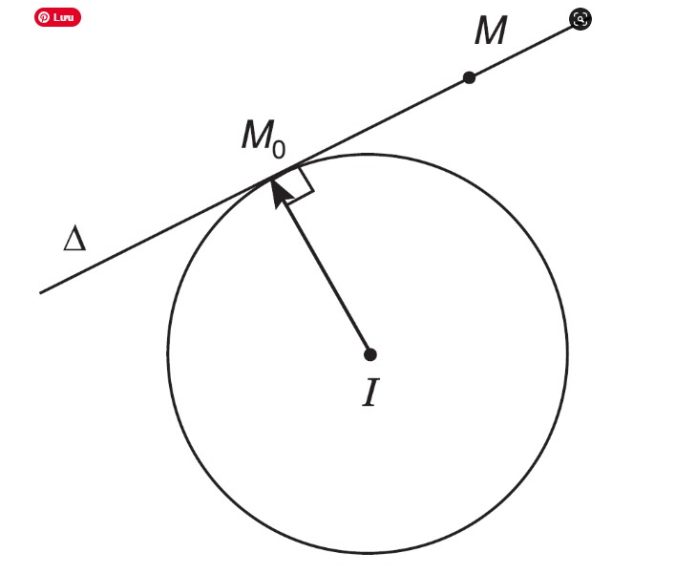
Phương trình đường tròn là một phương trình toán học mô tả một đường tròn trong không gian hai chiều.
* Cách xác định phương trình đường tròn
Để có thể nhận biết đâu là phương trình đường tròn thì các bạn sẽ dựa vào dạng đúng của phương trình đường tròn hoặc dựa vào điều kiện của phương trình đường tròn. Cụ thể như sau:
Cách 1: Các bạn chuyển phương trình đã cho về dạng: (2 – a)2 + (y−b)2 = R2 . Khi đó đường tròn đã cho có tâm là: I(a;b) và bán kính là R.
Cách 2: Các bạn chuyễn phương trình đã cho về dạng: x + y — 20 — 2by + c = 0 và chứng minh điều kiện a + b − c > 0 luôn đúng.
Cách 3: Dựa vào 2 dạng của phương trình đường tròn ở trên các bạn xem hệ số của x, y”. Nếu hai hệ số này bằng 1 hoặc có thể đưa chúng về hệ số củng bằng 1 thì sẽ có dạng phương trình đường tròn, sau đó tiếp tục dựa vào cách 1 hoặc cách 2 để chúng minh. Nếu hệ số x, y mà không biến đổi được về cùng bằng 1 thì các bạn có thể kết luận ngay phương trình đã cho không phải là phương trình đường tròn.
2. Cách viết phương trình đường tròn?
Để viết phương trình của một đường tròn, bạn cần biết tọa độ của tâm và bán kính của đường tròn. Phương trình đường tròn có dạng tổng quyền rộng nhất (phương trình tổng quyền hai) như sau:
(x – a)² + (y – b)² = r²
Trong đó:
- (x, y) là tọa độ của một điểm bất kỳ trên mặt phẳng.
- (a, b) là tọa độ của tâm của đường tròn.
- r là bán kính của đường tròn.
Dựa vào các giá trị cụ thể của (a, b) và r, bạn có thể viết phương trình cụ thể của đường tròn. Ví dụ, nếu bạn muốn viết phương trình của đường tròn có tâm ở điểm (3, 4) và bán kính là 5, phương trình đường tròn sẽ là:
(x – 3)² + (y – 4)² = 5²
Khi bạn biết tâm và bán kính của đường tròn, bạn có thể sử dụng phương trình này để mô tả và biểu diễn đường tròn đó trong không gian hai chiều.
3. Một số bài tập viết phương trình đường tròn khác:
* Viết phương trình đường tròn đi qua 3 điểm:
Cho đường tròn ( C) đi qua ba điểm A; B và C. Lập phương trình đường tròn đi qua ba điểm:
Gọi phương trình đường tròn là ( C): x2 + y2 – 2ax – 2by + c = 0 (*) ( với điều kiện a2 + b2 – c > 0).
Do điểm A; B và C thuộc đường tròn nên thay tọa độ điểm A; B và C vào (*) ta được phương trình ba phương trình ẩn a; b; c.
Giải hệ phương trình ba ẩn a; b; c ta được phương trình đường tròn.
* Viết phương trình đường tròn đường kính ab
Viết phương trình đường tròn đường kính AB biết A(4, −1); B(3, 5)

* Viết phương trình đường tròn ngoại tiếp tam giác abc
Viết pt đường tròn ngoại tiếp tam giác ABC biết A(3:-2) B(4;1) C(1;-3)
* Viết phương trình đường tròn qua 2 điểm
Viết phương trình đường tròn (C) trong biết (C) đi qua 2 điểm AB với A(1;1), B(5,3) và nhận AB là đường kính