1. Số nguyên tố là số gì?
Số nguyên tố là một loại số tự nhiên lớn hơn 1 và chỉ có hai ước số dương duy nhất là 1 và chính nó. Điều này có nghĩa rằng một số nguyên tố không thể chia hết cho bất kỳ số tự nhiên nào khác ngoài 1 và chính nó.
* Tính chất của số nguyên tố:
- 2 là số nguyên tố chẵn duy nhất. Đây cũng là số nguyên tố nhỏ nhất.
- Ước tự nhiên nhỏ nhất #1 của một số tự nhiên là số nguyên tố.
- Số nguyên tố là vô hạn.
- Tích của 2 số nguyên tố không thể là một số chính phương.
- Một tập hợp số c bất kỳ có ước nhỏ nhất là một số dương (x) với điều kiện x #1 và x< √c thì x là số nguyên tố.
2. Ví dụ về số nguyên tố?
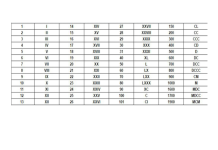
Ví dụ về các số nguyên tố đầu tiên là: 2, 3, 5, 7, 11, 13, 17, 19, 23, và tiếp tục. Số 2 là số nguyên tố duy nhất là số chẵn vì tất cả các số chẵn khác đều chia hết cho 2 ngoại trừ số 2.
Số nguyên tố có vai trò quan trọng trong toán học và các lĩnh vực khác như mã hóa, vật lý, và khoa học máy tính, và chúng thường được sử dụng trong việc phân tích và mã hóa thông tin.
3. Ký hiệu của số nguyên tố?
Ký hiệu của số nguyên tố thường được đặt là p, q, r, s, t hoặc các chữ cái khác trong bảng chữ cái.
4. Cách tìm số nguyên tố?
Cách 1: Kiểm tra số nguyên tố.
Nếu số đó nhỏ hơn 2 thì ta kết luận rằng đó không phải số nguyên tố.
Nếu số đó không có ước nào trong đoạn từ 2 đến căn bậc hai của n thì nó là số nguyên tố. Còn nếu số đó có ước trong đoạn từ 2 đến căn bậc hai của thì đó không phải là số nguyên tố.
Cách 2: Chia thử nghiệm.
Chia n cho tất cả các số nguyên từ 2 đến căn bậc hai của n. Nếu số nguyên nào chia hết cho n thì n là hợp số, còn không có thì n là số nguyên tố. ( số phép chia sẽ tăng dần theo cấp số nhân khi số chữ số của số nguyên đó ngày càng nhiều.)
Cách 3: Thao tác lặp từng phần tử với bước nhảy 1.
Để kiểm tra số n có phải là số nguyên tố hay không, ta cần áp dụng các bước sau:
Bước 1: Nhập vào số n.
Bước 2: Nếu số n nhỏ hơn 2 thì n không phải là số nguyên tố.
Bước 3: Lặp từ 2 tới (n-1), nếu trong khoảng này tồn tại số mà n không chia hết thì kết luận rằng số n là số nguyên tố, ngược lại nếu trong khoảng này số n chia hết thì số n không phải là số nguyên tố.
5. Bài tập ví dụ về số nguyên tố?
Ví dụ 1:
Trong các số dưới đây, số nào là số nguyên tố, số nào là hợp số? Vì sao?
- a:1 930
- b: 23
Đáp án
- a/ Số 1 930 là hợp số vì nó nhiều hơn 1 và có nhiều hơn 2 ước
- b/ Số 23 là số nguyên tố vì nó lớn hơn 1 và chỉ có 2 ước là 1 và chính nó.
Ví dụ 2:
Kiểm tra xem các số sau là hợp số hay số nguyên tố bằng cách dùng dấu hiệu của chia hết hoặc tra bảng số nguyên tố:
89 , 97 , 125 , 541 , 2 013 , 2 018
Đáp án
Các số nguyên tố là: 89 ; 97 ; 541
Các hợp số là: 125 ; 2 013; 2 018
Ví dụ 3:
- a/ Tìm số tự nhiên k để số 23k là số nguyên tố
- b/ Tại sao 2 là số nguyên tố chẵn duy nhất?
Đáp án
a/ Với k = 0 thì 23.k = 0 không là số nguyên tố với k = 1 thì 23.k = 23 là số nguyên tố.