1. Mặt phẳng là gì?
Trong toán học, mặt phẳng là một mặt hai chiều phẳng kéo dài vô hạn. Một mặt phẳng là mô hình hai chiều tương tự như một điểm (không chiều), một đường thẳng (một chiều) và không gian ba chiều.
Các mặt phẳng có thể xuất hiện như là không gian con của một không gian có chiều cao hơn, như là những bức tường của một căn phòng dài ra vô hạn, hoặc chúng có thể có quyền tồn tại độc lập, như trong các điều kiện của hình học Euclid.
(Trích: Wikipedia)
* Vậy nửa mặt phẳng là gì?
Hình gồm đường thẳng a và một phần của mặt phẳng bị chia cắt bởi a được gọi là nữa mặt phẳng bờ a.
Tính chất: Bất kì đường thẳng nào nằm trên mặt phẳng cũng là bờ chung của hai mặt phẳng đối nhau.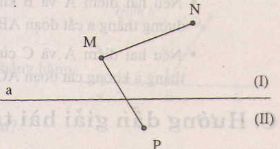
Trong hình trên: Nửa mặt phẳng (I) và nữa mặt phẳng(II) là hai nữa của một mặt phẳng đối nhau có bờ chung là a. – Hai điêm M,N thuộc nửa mặt phẳng (I) với MN không thuộc a thì đoạn thẳng MN không cắt a. – Hai điểm M,P thuộc hai nửa mặt phẳng đối nhau bờ a với M,P không thuộc a thì đoạn MP cắt a.
2. Phương trình mặt phẳng trong toán học
* Định nghĩa:
Phương trình Ax+By+Cz+D=0, trong đó A2+B2+C2≠0, được gọi là phương trình tổng quát của mặt phẳng.
Nhận xét:
a) (P): Ax+By+Cz+D=0 ⇒ (P) có 1 VTPT là n→=(A;B;C).
b) PT của (P) qua M0=(x0;y0;z0) và có VTPT n→=(A;B;C) là: A(x−x0)+B(y−y0)+C(z−z0)=0
Ví dụ 1: Cho mặt phẳng (P) có phương trình 2x+3y−z+2=0. Tìm một véctơ pháp tuyến của mặt phẳng.
Giải
Một véctơ pháp tuyến của (P) là n→=(2;3;−1) .
Ví dụ 2: Viết phương trình mặt phẳng đi qua điểm M0=(1;−2;3) và có vectơ pháp tuyến n→=(−2;1;4) .
Giải
Phương trình mặt phẳng (P) qua M0=(1;−2;3) và có VTPT n→=(−2;1;4) là:
−2(x−1)+1(y+2)+4(z−4)=0 ⇔ −2x+y+4z−12=0
Ví dụ về phương trình mặt phẳng trong toán học:
Ví dụ 1:
a) Đi qua điểm M(1; -2; 4) và nhận n→ = (2 ; 3 ; 5) làm vec tơ pháp tuyến
b) Đi qua A(0; -1; 2) và song song với giá của mỗi vec tơ u→ = (3; 2; 1) và v→ = (-3; 0; 1).
c) Đi qua ba điểm A(-3; 0; 0); B(0; -2; 0) và C(0; 0; -1).
Lời giải:
a) Mặt phẳng đi qua điểm M(1; -2; 4) và nhận n→ = (2; 3; 5) làm vectơ pháp tuyến là:
2(x – 1) + 3(y + 2) + 5(z – 4) = 0
⇔ 2x + 3y + 5z – 16 = 0.
b) Mặt phẳng nhận u→ và v→ là vec tơ chỉ phương
⇒ nhận 
= (2.1 – 1.0 ; 1.(-3) – 3.1 ; 3.0 – (-3).2) = (2; -6; 6) là vec tơ pháp tuyến.
Mặt phẳng đi qua A(0 ; -1 ; 2) nên có phương trình :
2(x – 0) – 6(y + 1) + 6(z – 2) = 0
⇔ 2x – 6y + 6z – 18 = 0
⇔ x – 3y + 3z – 9 = 0
c) 
Mặt phẳng (R) đi qua ba điểm A, B, C nhận 
là hai vec tơ chỉ phương
⇒ Nhận 
= ((-2).(-1) – 0; 0.3 – 3.(-1); 3.0 – 3.(-2)) = (2; 3; 6) là vec tơ pháp tuyến.
(R) đi qua A(-3; 0; 0) nên có phương trình:
2(x + 3) + 3y + 6z = 0
⇔ 2x + 3y + 6z + 6 = 0.
Ví dụ 2:
Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với A(2; 3; 7), B(4; 1; 3)
Lời giải:
