Nabla là gì trong toán học?

By
admin
-
0
3152
Nabla là gì trong toán học?

Mục lục bài viết

1. Nabla là gì ?

nabla, là một toán tử được sử dụng trong toán học, đặc biệt trong phép tính véc tơ, như một toán tử vi phân vectơ, thường được biểu thị bằng ký hiệu nabla. Khi được áp dụng cho một hàm được xác định trên miền một chiều, nó biểu thị đạo hàm chuẩn của nó như được định nghĩa trong phép tính.

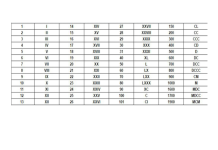
2.Vector Nabla trong tọa độ trụ:

\vec{\nabla}=\vec{i}\frac{\partial}{\partial x}+\vec{j}\frac{\partial}{\partial y}+\vec{k}\frac{\partial}{\partial z}, ta thay các biểu thức vector đơn vị và đạo hàm riêng tìm được ở trên vào, ta có được:

\vec{\nabla}=\vec{{e}_{r}}\frac{\partial}{\partial r}+\vec{{e}_{\theta }}\frac{1}{r}\frac{\partial}{\partial \theta }+\vec{{e}_{z}}\frac{\partial}{\partial z}

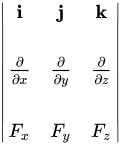
3. Vector Nabla trong tọa độ Descartes:

\vec{\nabla}=\vec{i}\frac{\partial}{\partial x}+\vec{j}\frac{\partial}{\partial y}+\vec{k}\frac{\partial}{\partial z}

4. Vector Nabla trong tọa độ trụ:

\vec{\nabla}=\vec{i}\frac{\partial}{\partial x}+\vec{j}\frac{\partial}{\partial y}+\vec{k}\frac{\partial}{\partial z}, ta thay các biểu thức vector đơn vị và đạo hàm riêng tìm được ở trên vào, ta có được:

\vec{\nabla}=\vec{{e}_{r}}\frac{\partial}{\partial r}+\vec{{e}_{\theta }}\frac{1}{r}\frac{\partial}{\partial \theta }+\vec{{e}_{z}}\frac{\partial}{\partial z}

>>> Dấu trong toán học

RELATED ARTICLESMORE FROM AUTHOR