n* nghĩa là gì trong toán học?

By
admin
-
6
8593
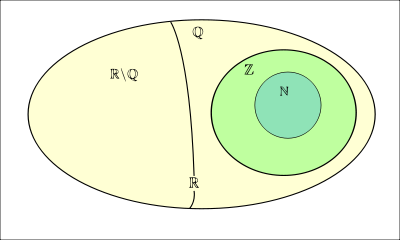
n* nghĩa là gì trong toán học?
n* nghĩa là gì trong toán học?
  • N: Tập hợp số tự nhiên
  • Z: Tập hợp số nguyên
  • Q: Tập hợp số hữu tỉ
  • I = R/Q: Tập hợp số vô tỉ
  • R: Tập hợp số thực

Chắc hẳn kí hiệu N là N* trong môn toán học đại số lớp 6 chúng ta đã bắt đầu học rồi đúng không? Và đó là kí hiệu theo mình là cũng khá quan trọng bạn nào quên thì có thể đọc nội dung bên dưới của mình để hiểu hơn nhé.

>>>: b là gì trong toán học?

1. Kí hiệu N và N* nghĩa là gì?

Trong toán học, số tự nhiên là tập hợp những số lớn hơn hoặc bằng 0, được ký hiệu là N. Các số 0, 1, 2, 3, 4, 5 là số tự nhiên, vì vậy ký hiệu tập hợp của nó sẽ là:

N = {0;1;2;3;4;5;...}

Vậy còn N*: Còn N* là tập hợp các số tự nhiên lớn hơn 0 (khác 0)

N* = {1;2;3;...} Hoặc N* = { }

2. Thứ tự trong tập hợp số tự nhiên

a) Số a nhỏ hơn số b, ta viết a < b hoặc b > a.
Để chỉ a > b hoặc a = b, ta viết a ≥ b.
a ≤ b nghĩa là
a < b hoặc a = b
Ví dụ:
1) Viết tập hợp bằng cách liệt kê các phần tử của nó
A = { 6; 7; 8; 9 }
2) Viết tập hợp B gồm các số nhỏ hơn 5 và lớn hơn 0 bằng 2 cách
B = { 1; 2; 3; 4 }
B = { x N / 1 ≤ x ≤ 4 }
b) Nếu a < b và b < c thì a < c.
Vd: Từ a < 2 và 2 < c thì suy ra
c) Mỗi số tự nhiên có một số liền sau duy nhất
Vd: Số liền sau của số 1 là số 2
a < c.
Số liền trước của số 2 là số 1

d) Số 0 là số tự nhiên nhỏ nhất. Không có số tự nhiên lớn nhất.

e) Tập hợp các số tự nhiên có vô số phần tử.

Chú ý: Hai số tự nhiên liên tiếp hơn kém nhau một đơn vị.

RELATED ARTICLESMORE FROM AUTHOR

6 COMMENTS

Comments are closed.