Định lý Pytago? Công thức định lý Pytago

Định lý pitago của ai? Tại sao lại có định lý Pytago này, công thức định lý pytago ra sao,…. sẽ được sieutonghop giải đáp cho các bạn nhé.

1. Định lý pytago?

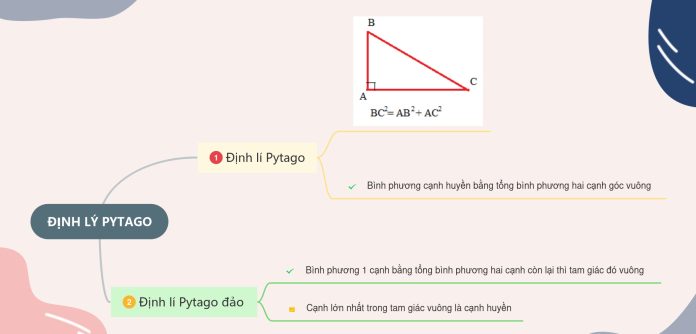
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

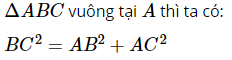
Ví dụ: Vẽ  tam giác vuông có hai cạnh góc vuông lần lượt bằng 3 và 4, Nhận xét tổng bình phương 2 cạnh góc vuông so với cạnh huyền.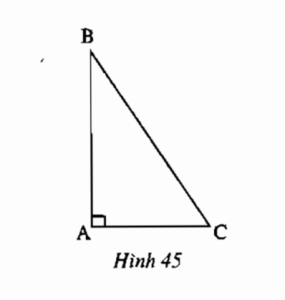

=> Ta thấy bình phương 2 cạnh góc vuông bằng bình phương cạnh huyền.

2. Định lý Pytago tiếng anh

3. Định lý Pytago đảo:

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

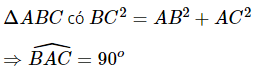
* Bài tập Áp dụng Định lý Pytago đảo:

Ví dụ: Cho tam giác ABC có AC= 5 cm, BC= 3 cm, AB= 4 cm. Tam giác ABC là tam giác gì?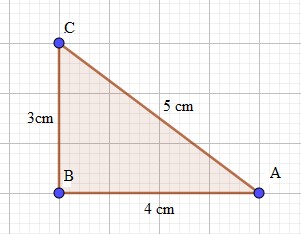

Ta có: $A{C}^2=B{C}^2+A{B}^2$( vì $5^2=3^2+4^2$)

Nên tam giác ABC vuông tại B( Định lí Pytago đảo).

Chú ý: Cạnh huyền là cạnh lớn nhất trong tam giác vuông

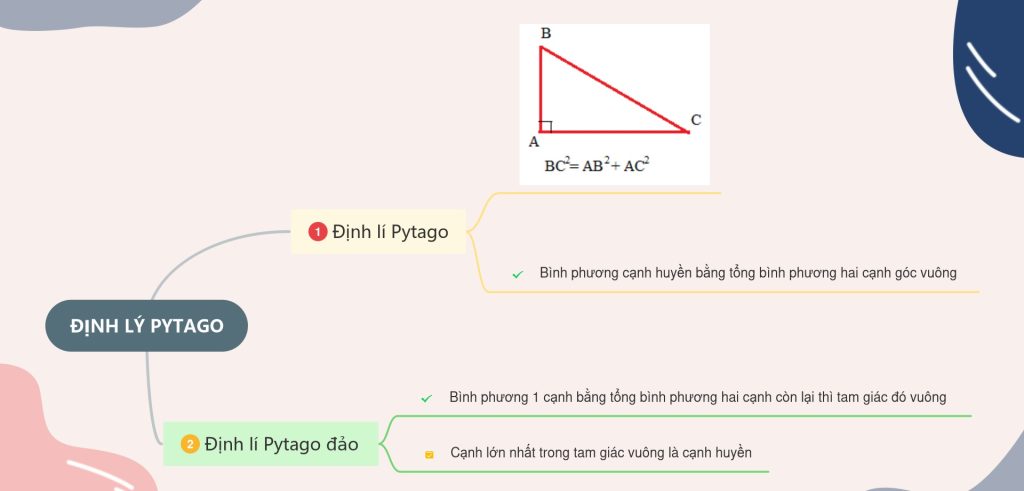
* Thêm ví dụ: Xét tam giác ABC vuông tại A:

1. Biết chiều dài cạnh AB = 4 cm, chiều dài cạnh BC = 6 cm, tính chiều dài cạnh AC
2. Biết chiều dài cạnh AC = 2 cm, chiều dài cạnh BC = 7 cm, tính chiều dài cạnh AB
3. Biết chiều dài cạnh AB = 3 cm, chiều dài cạnh AC = 5 cm, tính chiều dài cạnh BC

Lời giải

1. Ta có: BC² = AC² + AB²

=> AC² = BC² – AB²

=> AC² = 6² – 4²

=> AC = √20

Vậy chiều dài của cạnh AC là √20 cm

2. Ta có BC² = AC² + AB²

=> AB² = BC² – AC²

=> AB² = 7² – 2 ²

=> AB = √45

Vậy chiều dài cạnh AB = √45 cm

3. Ta có: BC² = AC² + AB²

=> BC² = 3² + 5²

=> BC = √34

Vậy chiều dài cạnh BC là√34