Q kí hiệu toán học nghĩa là gì? Tìm hiểu về Số hữu tỉ

Toán học – có rất nhiều các kí hiệu chữ cái Ví dụ như N, N*, Q, Z, I, R trong toán học và trong bài viết này mình sẽ cùng tìm hiểu về: “Q kí hiệu toán học” nhé!

1. Kí hiệu Q toán học trong toán học?

* Định nghĩa số hữu tỉ

Q trong toán học là số hữu tỉ (Kí hiệu Q) – là tập hợp các số có thể viết được dưới dạng phân số (thương số). Tức là một số hữu tỉ có thể được biểu diễn bằng một số thập phân vô hạn tuần hoàn. Số hữu tỉ được viết là a/b, trong đó a và b là các số nguyên nhưng b phải khác 0 Q là tập hợp các số hữu tỉ. Vậy ta có: Q={ a/b; a, b∈Z, b≠0}

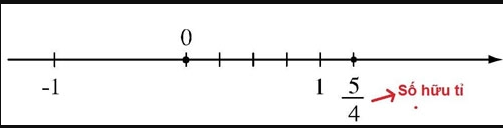
Ngoài ra còn một số kí hiệu toán học khác nữa ví dụ như:

Một số mối quan hệ các tập hợp số:

• N: Tập hợp số tự nhiên
• N*: Tập hợp số tự nhiên khác 0 – Kí hiệu N* trong toán học?
• Z: Tập hợp số nguyên – Kí hiệu Z là gì trong toán học?
• Q: Tập hợp số hữu tỉ
• I: Tập hợp số vô tỉ
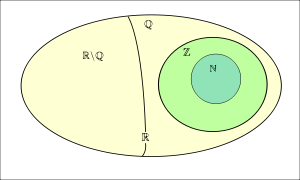
  Ta có : R = Q ∪ I. Tập N ; Z ; Q ; R.

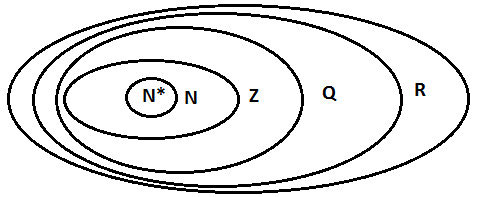
Khi đó quan hệ bao hàm giữa các tập hợp số là : N ⊂ Z ⊂ Q ⊂ R

Cần nắm vững ý nghĩa của từng kí hiệu :

• Kí hiệu ⊂ đọc là “tập hợp con của”.
• Kí hiệu N chỉ tập hợp các số tự nhiên.
• Kí hiệu Z chỉ tập hợp các số nguyên.
• Kí hiệu Q chỉ tập hợp các số hữu tỉ.

Tham khảo 1 số kí hiệu khác trong toán học bạn nên biết: 

• Kí hiệu B là gì trong toán học?
• Kí hiệu K là gì trong toán học?
• Kí hiệu e trong toán học
• Kí hiệu e ngược trong toán học
• Kí hiệu H trong toán học?
• Kí hiệu P trong toán học?
• Kí hiệu A trong toán học?
• Kí hiệu m trong toán học?

>>> r là bán kính hay đường kính?

>>> Hình chiếu trong toán học

2. Cách viết số hữu tỉ

Số hữu tỉ bao gồm số thập phân hữu hạn, số thập phân vô hạn tuần hoàn, tập hợp số nguyên. Bởi vậy, một số hữu tỉ có thể viết ở nhiều dạng: số thập phân, phân số. Đặc biệt với số hữu tỉ âm, có thể có 3 cách viết
VD: Nêu ba cách viết của số hữu tỉ -3/5?

• Dạng phân số có thể viết: -3/5; 3/-5
• Dạng số thập phân: -0,6

3. Một số bài tập ví dụ: 

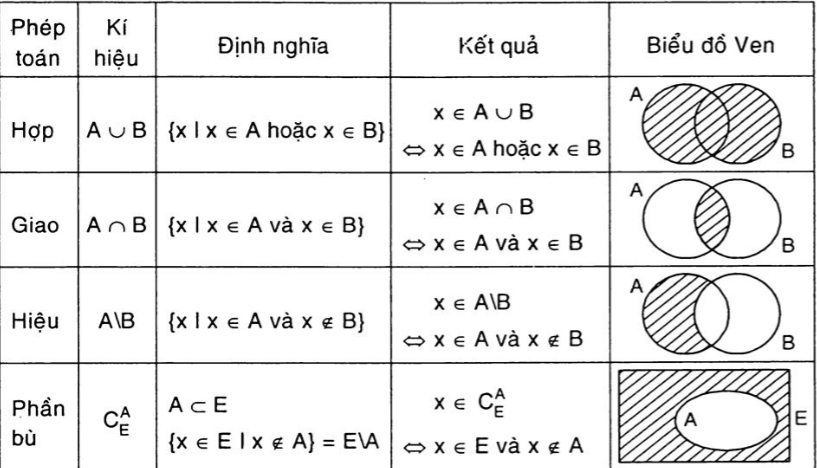
Bài 1: Chọn câu trả lời đúng trong các câu sau:

a) [a;b] ⊂ (a;b]
b) [a;b) ⊂ (a;b]
c) [a;b] ⊂ (a;b)
d) (a;b], [a;b) đều là tập con của [a;b]

Giải:

Chọn đáp án D. vì [a;b] là tập lớn nhất trong 4 tập hợp:

Bài 2:  Xác định mỗi tập hợp sau: 

a) [-2;4)∪(0;5]

b) (-1;6]∩[1;7)

c) (-∞;7)\(1;9)

Giải:

a) [-2;4)∪(0;5]=[-2;5]

b) (-1;6]∩[1;7)=[1;6]

c) (-∞;7)\(1;9)=(-∞;1]

Đây là dạng toán thường gặp nhất, để giải nhanh dạng toán này ta cần vẽ các tập hợp lên trục số thực trước, phần lấy ta sẽ giữa nguyên còn phần không lấy ta sẽ gạch bỏ đi. Sau đó việc lấy giao, hợp hay hiệu sẽ dễ dàng hơn.

Bài 3: Xác định mỗi tập hợp sau

a) (-∞;1]∩(1;2)

b) (-5;7]∩[3;8)

c) (-5;2)∪[-1;4]

d) (-3;2)\[0;3]

e) R\(-∞;9)

Giải:

a) (-∞;1]∩(1;2) ≠ ∅

b) (-5;7]∩[3;8) = [3;7)

c) (-5;2)∪[-1;4] = (-1;2)

d) (-3;2)\[0;3] = (-3;0]

e) R\(-∞;9) = [9;+∞)

Bài 4: Xác định các tập hợp sau bằng cách liệt kê

Bài 5: Liệt kê các phần tử của các tập hợp sau đây

Bài 6: Xác định các tập hợp sau và biểu diễn chúng trên trục số

a) [-3;1) ∪ (0;4]

b) [-3;1) ∩ (0;4]

c) (-∞;1) ∪ (2;+∞)

d) (-∞;1) ∩ (2;+∞)

Bài 7:

A=(-2;3) và B=[1;5]. Xác định các tập hợp: A ∪ B, A ∩ B, A\B, B\A.

Bài 8: 

Cho A={x € R||x ≤ 4}; B={x€ R|-2 ≤ x+1 < 3}

Viết các tập sau dưới dạng khoảng – đoạn – nửa khoảng: A ∩ B, A\B, B\A, R\(A∪B)

Bài 9:

Cho A={x € R|-3 ≤ x ≤ 5} và B = {x € Z|-1< x ≤ 5}

Xác định các tập hợp: A ∪ B, A ∩ B, A\B, B\A

Bài 10:

Cho và A={x € R|x>2} và B={x € R|-1 < x ≤ 5}

Xác định các tập hợp: A ∪ B, A ∩ B, A\B, B\A

Bài 11:

Cho A={2,7} và B=(-3,5].  Xác định các tập hợp: A ∪ B, A ∩ B, A\B, B\A

Bài 12:

Xác định các tập hợp sau và biểu diễn chúng trên trục số

a) R\((0;1) ∪ (2;3))

b) R\((3;5) ∩ (4;6)

c) (-2;7)\[1;3]

d) ((-1;2) ∪ (3;5))\(1;4)

Bài 13:

Cho A={x € R| 1 ≤ x ≤ 5}, B={x € R| 4 ≤ x ≤ 7} và C={x € R| 2 ≤ x < 6}.

a) Xác định các tập hợp:
b) Gọi D ={x € R| a ≤ x ≤ b}. Xác định a, b để D⊂A∩B∩C

Bài 14:

Viết phần bù trong R các tập hợp sau:

A={x € R|-2 ≤ x < 10}

B={x € R||x| > 2}

C={x € R|-4< x + 2 ≤ 5}

Bài 15:

Cho A = {x € R|x ≤ -3 hoặc x > 6}, B={x€ R|x²– 25 ≤ 0}

a) Tìm khoảng – đoạn – nửa khoảng sau đây: A\B, B\A, R\(A ∪ B), R\(A∩B), R\(A\B)
b) Cho C={x € R|x≤a}; D={x € R|x ≥b}. Xác định a,b biết rằng C∩BvμD∩B là các đoạn có chiều dài lần lượt là 7 và 9. Tìm C∩D.

Bài 16:

Cho các tập hợp

A={x € R|-3 ≤ x ≤ 2}

B= {x € R|0 ≤ x ≤ 7}

C= {x € R|x ≤ -1}

D= {x € R|x ≥ 5}

a) Dùng kí hiệu đoạn, khoảng, nửa khoảng để viết lại các tập hợp trên
b) Biểu diễn các tập hợp A, B, C, D trên trục số

Cuối cùng:

Như vậy là bài viết này mình đã hướng dẫn các bạn về số hữu tỉ cũng như Kí hiệu Q trong toán học – rồi đúng không? Hi vọng đã đem đến cho các bạn các kiến thức bổ ích.

>>> Dấu trong toán học