Quỹ tích là gì? Bài tập ví dụ về quỹ tích lớp 9?

1. Quỹ tích là gì?

Một hình H được gọi là quỹ tích của điểm M sẽ có tính chất T khi và chỉ khi hình H chứa các điểm có tính chất T.

Các loại quỹ tích cơ bản:

• Tập hợp các điểm bao gồm hai điểm A, B và tất cả những điểm nằm giữa A và B là đoạn thẳng AB.
• Tập hợp các điểm cách đều hai điểm cố định chính là đường trung trực của đoạn thẳng nối hai điểm ấy.
• Tập hợp các điểm cách đều hai cạnh của một góc chính là tia phân giác của góc đó.
• Tập hợp các điểm cách đường thẳng (d) một khoảng bằng I là hai đường thẳng song song với (d) và sẽ cách đường thẳng (d) một khoảng chính bằng I.
• Ta có tập hợp của các điểm cách điểm cố định O một khoảng bằng R chính là đường tròn tâm O, với bán kính R trong mặt phẳng và là mặt cầu tâm O, bán kính R trong không gian ba chiều.
• Tập hợp các điểm M tạo với hai đầu mút của đoạn thẳng AB cho trước một góc AMBˆ sẽ có số đo bằng α không đổi là hai cung tròn đối xứng nhau qua AB (được gọi là cung tròn chứa góc α vẽ trên đoạn AB).
• Tập hợp những cặp điểm đối xứng nhau qua một đường thẳng là mặt phẳng chứa đường thẳng đó.
• Tập hợp các điểm trong mặt phẳng với tổng khoảng cách tới hai điểm cố định cho trước (nằm trong mặt phẳng đó) chính là đường elíp nhận hai điểm cố định đó là tiêu điểm.
• Tập hợp các điểm cách đều một điểm và một đường thẳng cố định sẽ là đường Parabol trong mặt phẳng đi qua điểm và đường cố định đó.

– Cách chuẩn bị giải bài toán quỹ tích

Trước hết bạn cần tìm hiểu kĩ bài toán để nắm vững các yếu tố đặc trưng cho bài toán. Trong một bài toán quỹ tích thường sẽ xuất hiện 3 yếu tố sau đây:

• Yếu tố cố định: Như các điểm, đoạn thẳng hay đường thẳng, ….
• Yếu tố không đổi: Như độ dài đoạn thẳng, độ lớn của góc, ….
• Yếu tố thay đổi: Thông thường là các điểm mà ta cần tìm quỹ tích, hoặc các đoạn thẳng, hoặc các hình mà trên đó chứa các điểm ta cần tìm quỹ tích.

2. Ví dụ về quỹ tích lớp 9?

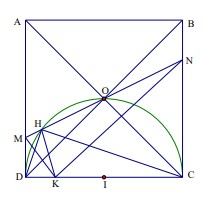
Ví dụ 1: Cho hình vuông ABCD có tâm O. Một đường thẳng xy quanh O cắt hai cạnh AD
và BC lần lượt tại M và N. Trên CD lấy điểm K sao cho DK DM = . Gọi H là hình chiếu của
K trên xy. Tìm quĩ tích của điểm H.

Lời giải: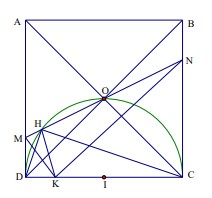

• Phần thuận: Ta có CN AM = . Vì DK DM = nên.
Các tứ giác MHKD, NHKC nội tiếp đường tròn nên

Vậy điểm H nằm trên đường tròn đường kính CD.
• Giới hạn: Điểm H chỉ nằm trên một nửa đường
tròn đường kính CD nằm trong hình vuông.
• Phần đảo: Lấy điểm H bất kỳ trên nửa đường tròn
đường kính CD. Vẽ đường thẳng HO cắt cạnh AB,
BC lần lượt tại M và N. Lấy K trên CD sao cho DK =
DM, ta phải chứng minh H là hình chiếu của K trên
MN.

Ví dụ 2: Cho đường tròn ( ) O; R cố định. Lấy B, C là hai điểm cố định trên đường tròn và
A là một điểm tuỳ ý trên đường tròn. Gọi M là điểm đối xứng của điểm C qua trung điểm
I của AB. Tìm quỹ tích các điểm M.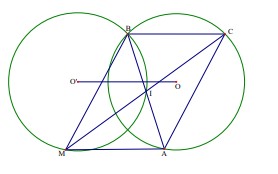

• Phần thuận: Kẻ OO’// BC và OO’ BC = (O’ và
B trên cùng một nửa mặt phẳng bờ AC). Do đó
ta được O’ cố định (vì O, B, C cố định và BC
không đổi)
Tứ giác AMBC là hình bình hành (vì I là trung
điểm của hai đường chéo AB và MC). Suy ra
MA // BC và MA BC = , mà ta lại có OO’// BC
và OO’ BC =
Do đó ta được MA // OO’ và MA OO’ =
Từ đó ta được tứ giác AMO’O là hình bình
hành (dhnb)
Nên suy ra O’M OA R = = không đổi và O’ cố
định
Vậy khi A di động thì M di động theo nhưng M luôn cách O’ cố định một khoảng không
đổi là O’M OA R = = . Nên M thuộc đường tròn tâm O’ bán kính OA R= .
• Giới hạn: khi A di động thì M di động trên đường tròn tâm O’ bán kính OA R= .
• Phần đảo: Trên đường tròn ( ) O’, R lấy điểm M bất kỳ. Nối MB. Qua C kẻ đường thẳng
song song với BM cắt đường tròn (O) ở điểm thứ hai A. Ta dễ dàng chứng minh được M
đối xứng với C qua trung điểm I của AB
• Kết luận: Vậy khi A di động thì M di động theo nhưng M luôn cách O’ cố định một
khoảng không đổi là O’M OA R = = . Nên quỹ tích điểm M là đường tròn tâm O’ bán kính
OA = R

Ví dụ 3: Cho ba điểm ABC cố định và thẳng hàng theo thứ tự đó. Trên đường thẳng d
vuông góc với AB tại B lấy điểm D bất kì. Gọi H là trực tâm tam giác DAC. Tìm quỹ tích
điểm O là tâm của đường tròn ngoại tiếp tam giác ADH.

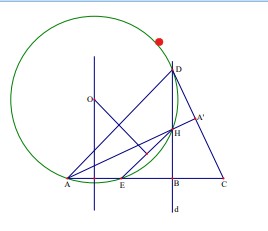
Phần thuận: Gọi giao điểm thứ hai của đường
tròn (O) với AC là E.

Mà E thuộc đường thẳng cố định và B cố định nên E là điểm cố định.
Ta có OA OE = nên O thuộc đường thẳng cố định là đường trung trực của đoạn thẳng AE.
• Giới hạn: Khi D di động trên đường thẳng d thì O di động trên đường trung trực của
đoạn thẳng AE, trừ trung điểm M của đoạn thẳng AE.
• Phần đảo: Lấy điểm O bất kì trên đường trung trực của đoạn thẳng AE(không trùng với
trung điểm của AE). Vẽ đường tròn tâm O bán kính OA cắt đường thẳng d tại các điểm H,
D.
Do OA OE = nên E nằm trên đường tròn (O)

Các bạn có thể tìm thêm một số Bài tập ví dụ về quỹ tích lớp 9? ở link bên dưới:

Download (PDF, 2.93MB)