Delta trong toán học là gì?

1. Delta trong toán học là gì?

Delta là một kí hiệu chữ La Tinh chỉ một biệt số trong phương trình bậc hai. Dựa vào từng giá trị của delta thì ta có thể kết luận phương trình bậc hai đó có nghiệm hay không.

Thêm vào nữa là định lí Viet, giá trị của delta và công thức Viét sẽ chững minh cho ta phương trình đó có 1 nghiệm hay 2 nghiệm hoặc vô nghiệm,dấu của hai nghiệm đó như thế nào,cùng dấu hay trái dấu.

Nếu delta>0 thì phương trình bậc hai có 2 nghiệm phân biệt.

• “Delta = 0 thì có 1 nghiệm kép
• Delta < 0 thì vô nghiệm”.

Cho phương trình bậc hai ax^2+bx+c=0 thì delta=b^2-4ac. Nếu giá trị b là một số chẵn thì delta sẽ đc rút gọn thành delta phẩy=(b/2)^2-ac.
Đó là những cái cơ bản về delta, ngoài ra delta còn dùng để chững minh phương trình có nghiệm, xác định đỉnh của parabol mà lớp 10 bạn sẽ học. Trong hình học delta còn dùng để kí hiệu đường thẳng.

2. Ví dụ về công thức tính Delta trong toán học?

Phương trình bậc 2 là phương trình có dạng:

ax² + bx + c = 0

Trong đó: a ≠ 0 , a , b là hệ số, c là hằng số

Công thức nghiệm:

Ta xét phương trình: ax² + bx +c = 0

Với biệt thức delta: Δ = b² – 4ac.  Sẽ có 3 trường hợp:

Trong trường hợp nếu b = 2b’ thì các bạn có thể tính delta phẩy, công thức như sau:

• Nếu Δ < 0 thì phương trình vô nghiệm
• Nếu Δ = 0 thì phương trình có nghiệm kép:
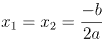
• Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt:

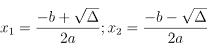
Công thức tính delta phẩy

Ta xét phương trình: ax² + bx +c = 0. Với biệt thức delta phẩy: Δ′ = b′² – ac. Trong đó: 

→ Công thức trên còn được gọi là công thức nghiệm thu gọn. Tương tự như delta thì delta phẩy chúng ta cũng có 3 trường hơp bao gồm:

• Nếu Δ′ < 0  thì phương trình vô nghiệm
• Nếu Δ′ = 0 thì phương trình có nghiệm kép:
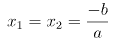
• Nếu Δ′ > 0 thì phương trình có hai nghiệm phân biệt:

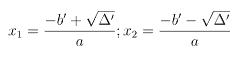
3. Bài tập vận dụng 

Bài 1: Cho phương trình x² – 2(m+1)x + m² + m +1 = 0

• Tìm các giá trị của m để phương trình có nghiệm
• Trong trường hợp phương trình có nghiệm là x1, x2 hãy tính theo m

Bài 2: Chứng minh rằng phương trình sau có nghiệm với mọi a, b:

(a+1) x² – 2 (a + b)x + (b- 1) = 0

Bài 3:  Giả sử phương trình bậc hai x² + ax + b + 1 = 0 có hai nghiệm dương. Chứng minh rằng a² + b² là một hợp số.

Bài 4: Cho phương trình (2m – 1)x² – 2(m + 4 )x +5m + 2 = 0 (m #½)

• Tìm giá trị của m để phương trình có nghiệm.
• Khi phương trình có nghiệm x1, x2, hãy tính tổng S và tích P của hai nghiệm theo m.

Tìm hệ thức giữa S và P sao cho trong hệ thức này không có m.

Bài 5: Cho phương trình x² – 6x + m = 0. Tính giá trị của m, biết rằng phương trình có hai nghiệm x1, x2 thỏa mãn điều kiện x1 – x2 = 4.

Bài 6: Cho phương trình bậc hai: 2x² + (2m – 1)x +m – 1 =0

• Chứng minh rằng phương trình luôn luôn có nghiệm với mọi m.
• Xác định m để phương trình có nghiệm kép. Tìm nghiệm đó.
• Xác định m để phương trình có hai nghiệm phan biệt x1, x2 thỏa mãn -1 < x1 < x2 < 1

Trong trường hợp phương trình có hai nghiệm phân biệt x1, x2, hãy lập một hệ thức giữa x1, x2 không có m.

Bài 7: Cho f(x) = x² – 2(m +2)x+ 6m +1

Chứng minh rằng pt f(x) = 0 luôn nghiệm với mọi m.

Đặt x = t + 2; tình f(x) theo t. Từ đó tìm điều kiện của m để phương trình f(x) = 0 có hai nghiệm phân biệt lớn hơn 2.

Bài 8: Cho tam thức bậc hai f(x) = ax² + bx +c thỏa mãn điều kiện Ι f(x)Ι  =< 1 với mọi x ∈ { -1; 1 }. Tìm GTNN của biểu thức A= 4a² + 3b².

Bài 9: Cho phương trình (x²)² – 13 x² + m = 0. Tìm các giá trị của m để phương trình:

• a. Có bốn nghiệm phân biệt.
• b. Có ba nghiệm phân biệt.
• c. Có hai nghiệm phân biệt.
• d. Có một nghiệm
• e. Vô nghiệm.

4. Kết luận

Ok vậy là vậy là mình đã View xong cho các bạn về “Delta trong toán học” Chúc các bạn có các kiến thức bổ ích.

>> Xem thêm: Các dấu trong toán học