Các dấu trong toán học bạn cần biết?

By
admin
-
23
6405
Các dấu trong toán học bạn cần biết?

Trong toán học sẽ có rất nhiều các kí hiệu đặc biệt là các dấu ngoặc, dấu ngoặc đơn, dấu ngoặc nhọn và dấu ngoặc nhọn,…. Và chúng ta sẽ không biết sẽ dùng khi nào và ở đâu! Cho nên bài viết này mình sẽ tổng hợp các dấu trong toán học cho các bạn cùng biết.

1. Bảng kí hiệu các dấu trong toán học

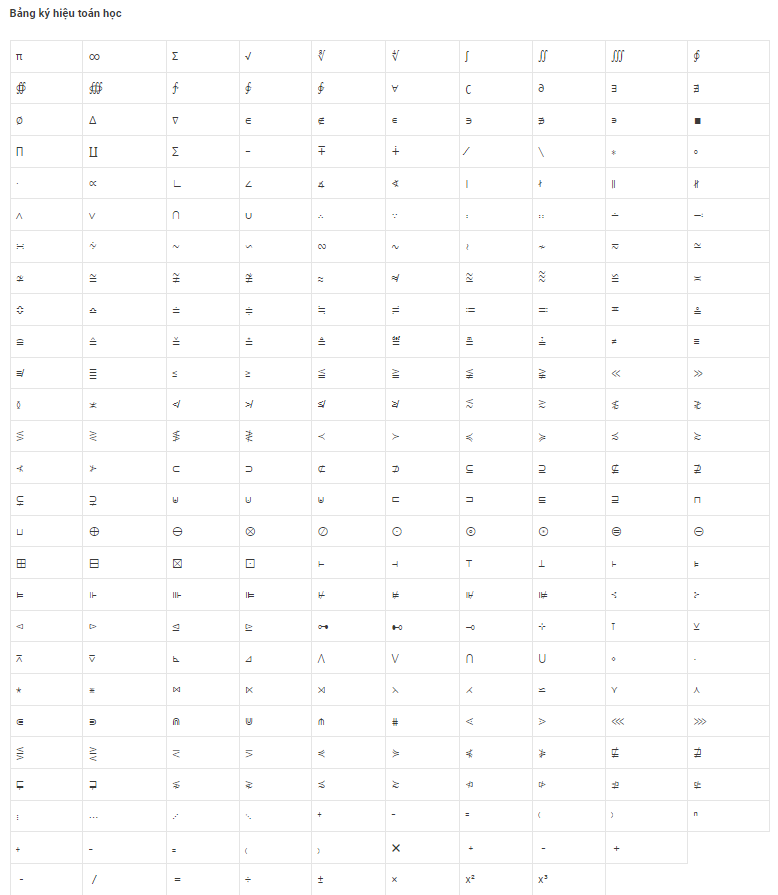
Như trên bảng kí hiệu hóa học trên mình sẽ tóm tắt một số dấu, kí hiệu trong toán học cho các bạn:

Biểu tượng                                     Nội dung 
+ Thêm dấu: Thường được gọi là dấu cộng hoặc dấu cộng
– Dấu trừ: Thường được gọi là dấu trừ
x Dấu nhân : Thường được gọi là dấu thời gian hoặc bảng thời gian
÷ Dấu hiệu phân chia: Để phân chia
= Dấu bằng
| | Giá trị tuyệt đối
≠ Không bằng
() Dấu ngoặc đơn
[] Dấu ngoặc vuông
% Dấu phần trăm: Trên 100
∑ Dấu hiệu tổng lớn: Tính tổng
√ Dấu căn bậc hai
< Dấu hiệu bất đẳng thức: Nhỏ hơn
> Dấu hiệu bất đẳng thức: Lớn hơn
! yếu tố
θ Theta
π Số Pi
≅ Xấp xỉ
∅ Bộ trống
∠ Dấu góc
! Dấu hiệu giai thừa
∴ vì thế
∞ vô cực

Dưới đây là danh sách đầy đủ 24 chữ cái trong bảng chữ cái Hy Lạp thường được sử dụng trong các bộ môn Toán, Lý, Hóa. và cách đọc ký hiệu toán học

  • Α α (Alpha)
  • Β β (Beta)
  • Γ γ (Gamma)
  • Δ δ (Delta)
  • Ε ε (Epsilon)
  • Ζ ζ (Zeta)
  • Η η (Eta)
  • Θ θ (Theta)
  • Ι ι (Iota)
  • Κ κ (Kappa)
  • Λ λ (Lambda)
  • Μ μ (Mu)
  • Ν ν (Nu)
  • Ξ ξ (Xi)
  • Ο ο (Omicron)
  • Π π (Pi)
  • Ρ ρ (Rho)
  • Σ σ ς (Sigma)
  • Τ τ (Tau)
  • Υ υ (Upsilon)
  • Φ φ (Phi)
  • Χ χ (Chi)
  • Ψ ψ (Psi)
  • Ω ω (Omega)

2. Ý nghĩa dấu ngoặc trong toán học?

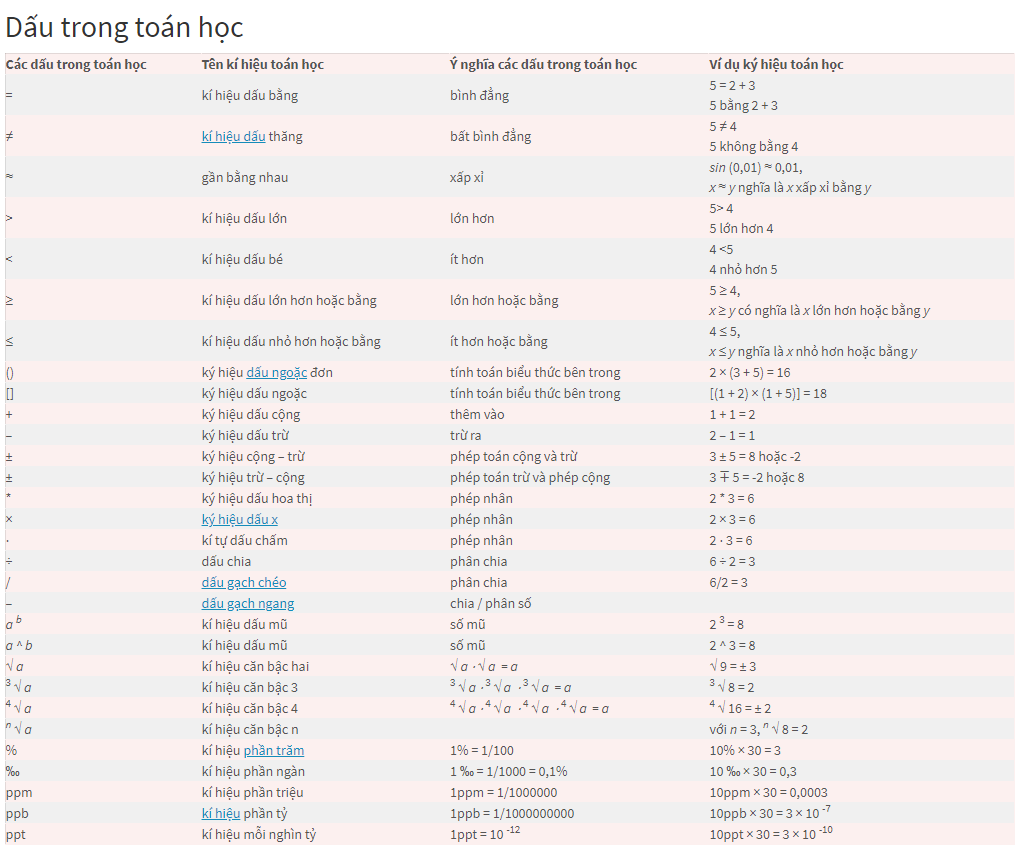
* Sử dụng dấu ngoặc đơn ()

Dấu ngoặc đơn được sử dụng để nhóm các số hoặc biến hoặc cả hai. Khi bạn thấy một bài toán có chứa dấu ngoặc, bạn cần sử dụng thứ tự các phép toán để giải nó. Ví dụ, giải bài toán: 9 – 5 ÷ (8 – 3) x 2 + 6

Đối với vấn đề này, trước tiên bạn phải tính toán hoạt động trong dấu ngoặc đơn — ngay cả khi đó là một phép toán thường xuất hiện sau các phép toán khác trong bài toán. Trong bài toán này, các phép toán nhân và chia thông thường sẽ đứng trước phép trừ (trừ), tuy nhiên, vì 8 – 3 nằm trong dấu ngoặc đơn, bạn nên giải phần này của bài toán trước. Khi bạn đã quan tâm đến phép tính nằm trong dấu ngoặc đơn, bạn sẽ xóa chúng. Trong trường hợp này (8 – 3) trở thành 5, vì vậy bạn sẽ giải quyết vấn đề như sau:

9 – 5 ÷ (8 – 3) x 2 + 6

= 9 – 5 ÷ 5 x 2 + 6

= 9 – 1 x 2 + 6

= 9 – 2 + 6

= 7 + 6

= 13

Lưu ý rằng theo thứ tự của các phép toán, bạn sẽ tính toán những gì trong ngoặc đơn trước tiên, tiếp theo, tính toán các số với số mũ, sau đó nhân và / hoặc chia, và cuối cùng, cộng hoặc trừ. Nhân và chia, cũng như cộng và trừ, giữ một vị trí ngang nhau theo thứ tự các phép toán, vì vậy bạn thực hiện các phép toán này từ trái sang phải.

Trong bài toán trên, sau khi thực hiện phép trừ trong ngoặc, trước tiên bạn cần chia 5 cho 5, thu được 1; sau đó nhân 1 với 2, thu được 2; sau đó trừ 2 với 9, thu được 7; và sau đó thêm 7 và 6, tạo ra câu trả lời cuối cùng là 13.

* Dấu ngoặc đơn cũng có thể có nghĩa là phép nhân

Trong bài toán: 3 (2 + 5), dấu ngoặc đơn cho bạn biết nhân. Tuy nhiên, bạn sẽ không nhân cho đến khi hoàn thành thao tác bên trong dấu ngoặc đơn — 2 + 5 — vì vậy bạn sẽ giải quyết vấn đề như sau:

3 (2 + 5)

= 3 (7)

= 21

* Ví dụ về Dấu ngoặc []

Dấu ngoặc được sử dụng sau dấu ngoặc đơn để nhóm các số và biến. Thông thường, bạn sẽ sử dụng dấu ngoặc đơn trước, sau đó đến dấu ngoặc, tiếp theo là dấu ngoặc nhọn. Dưới đây là một ví dụ về sự cố khi sử dụng dấu ngoặc:

 4 – 3 [4 – 2 (6 – 3)] ÷ 3

= 4 – 3 [4 – 2 (3)] ÷ 3 (Thực hiện thao tác trong dấu ngoặc đơn trước; bỏ dấu ngoặc đơn.)

= 4 – 3 [4 – 6] ÷ 3 (Thực hiện thao tác trong dấu ngoặc.)

= 4 – 3 [-2] ÷ 3 (Dấu ngoặc cho biết bạn nhân số trong đó, là -3 x -2.)

= 4 + 6 ÷ 3

= 4 + 2

= 6

* Ví dụ về dấu ngoặc nhọn {}

Dấu ngoặc nhọn cũng được sử dụng để nhóm các số và biến. Bài toán ví dụ này sử dụng dấu ngoặc đơn, dấu ngoặc và dấu ngoặc nhọn. Dấu ngoặc đơn bên trong các dấu ngoặc đơn khác (hoặc dấu ngoặc nhọn và dấu ngoặc nhọn) cũng được gọi là ” dấu ngoặc đơn lồng nhau .” Hãy nhớ rằng, khi bạn có dấu ngoặc đơn bên trong dấu ngoặc nhọn và dấu ngoặc nhọn hoặc dấu ngoặc đơn lồng nhau, hãy luôn làm việc từ trong ra ngoài:

 2 {1 + [4 (2 + 1) + 3]}

= 2 {1 + [4 (3) + 3]}

= 2 {1 + [12 + 3]}

= 2 {1 + [15]}

= 2 {16}

= 32

* Ghi chú về Dấu ngoặc đơn, Dấu ngoặc và Dấu ngoặc

Dấu ngoặc đơn, dấu ngoặc nhọn và dấu ngoặc nhọn đôi khi được gọi tương ứng là dấu ngoặc vuông “tròn”, “vuông” và “xoăn”. Dấu ngoặc nhọn cũng được sử dụng theo bộ, như trong:

{2, 3, 6, 8, 10 …}

Khi làm việc với lồng đơn dấu ngoặc, các thứ tự sẽ luôn là đơn dấu ngoặc, dấu ngoặc nhọn, dấu ngoặc nhọn. (Trích: Loigiaihay)

Một số bài viết về “học thuật” liên quan :

RELATED ARTICLESMORE FROM AUTHOR

23 COMMENTS

Comments are closed.